geometria analityczna
Madzik: dane są dwa punkty A=(−3,8), B=(2,2) . wyznacz wspolrzedne takiego punktu nalezacego do osi ox
aby suma kwadratow długosc odcinkow AM i MB była najmniejsza
4 lis 20:22
Bizon:
f(x
M)=(−3−x
M)
2+(8−0)
2+(2−x
M)
2+(2−0)
2
f(x
M)=9+6x
M+x
M2+64+4−4x
M+x
M2+4
f(x
M)=2x
M2+2x
M+81
4 lis 20:41
Madzik: nie bardzo rozumiem...
4 lis 20:49
Bizon:
... a czego nie rozumiesz
Skoro punkt leży na osi 0x to ma współrzędne M=(xM, 0}
Wzór na długość odcinka znasz ...
Potem już tylko analiza funkcji kwadratowej
4 lis 21:03
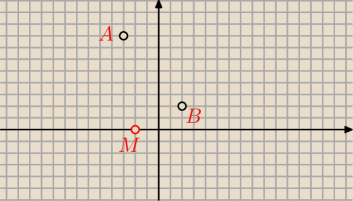
Madzik: ale wzór na długość odcinka ma jeszce pierwiasek i ten punk M zaznaczony na wykresie nie zgadza
sie z wyliczonym xM=−12
4 lis 21:25
Bizon:
... ten punkt zaznaczyłem tylko poglądowo
a skoro masz sumę kwadratów długości ... to pierwiastki out
4 lis 21:28
Madzik: nooo chyba ze tak
4 lis 21:29
Madzik: hmm tylko jeszcze nie rozumiem co nastapilo miedzy 3 a 4 linijka obliczen, Δ wychodzi ujemna...
4 lis 21:41