Mila :D ! Hugo: Z talii 52 kart losowo odłożono: a)jedną kartę b)5 kart c) 51 kart d) k kart a następnie z pozostałych kart wylosowano 1 kartę. Jakie jest prawdopodobieństwo że wylosowana kartą jest as kier?

miko: a) szansa na as kier jest 1:52→ zostało 52−1=51→ szansa na as kier ⁵¹_52*51

Hugo: Nie bez pośrednio Bo jak nam wyrzucą na początku asa kiera to po zabawie :C na moje rozumowanie 51/52*1/52 : )) (51 kart bez asa kier razy szansa na niego w wylosowaniu) // Prawdopodobieństwo Całkowite się kłania. Omawiam dopiero jutro ale zrozumcie, taki cep jak ja co ma dopa jak by jutro tak wszystkich wydymał swą wiedzą :3 ♥♥♥.... P(A) = P(A/B) * P(B) + P(A/b) * P(b) w teorii A − wylosowano kiera Asa B − ? b − ?

Hugo: xD wgl to może być w 1 na 52 przypadki PRAWDOPODOBIEŃSTWO WARUNKOWE ! obalcie mi; { If(wylosujemy pika asa value=1) { nie wylosujemy już go :_: print('Warunkowe') }; else( to jednak prawdopodobieństwo całkowite :3) { }; };

Mila: a) dobrze To nie jest typowe zadanie z prawdopodobieństwa całkowitego. Wybierz inne, albo ja Ci napiszę.

Hugo: W końcu jest moja zbawczyni!. nadzieja powróciła : ) Ale możesz mi to rozpisać na ' prawd całkowite' ? bo tak na chłopski to moze zawsze jakoś a potem 0pkt ; / + czy mam racje z tym że w 1 przypadku będzie warunkowe prawdopodobieństwo? Wiec kolejne i dz za uznanie że mi sie coś udało to pociesza : )

Hugo: W końcu jest moja zbawczyni!. nadzieja powróciła : ) Ale możesz mi to rozpisać na ' prawd całkowite' ? bo tak na chłopski to moze zawsze jakoś a potem 0pkt ; / + czy mam racje z tym że w 1 przypadku będzie warunkowe prawdopodobieństwo? Wiec kolejne i dz za uznanie że mi sie coś udało to pociesza : )

Hugo: Z grupy 20 mężczyzn i 30 kobiet losujemy dwie osoby a następnie z tych dwóch osób wybieramy również w sposób losowy jedną. Jakie jest prawdopodobieństwo że wybierzemy mężczyznę? A − wybraliśmy mężczyznę B − hmm B(dwa) => oznaczmy małe 'b' − hmmm xD? z pewnoscią tu bym dał warunek 1 z dwóch tych ów osób ale dalej leże i kwiczę. cyt Mówiąc zaz­wyczaj, ma­my na myśli zaw­sze, które zaz­wyczaj się sprawdza.

Mila: W tych zadaniach można się wspomagać drzewkiem. Z talii 52 kart losowo odłożono: b)5 kart a następnie z pozostałych kart wylosowano 1 kartę. Jakie jest prawdopodobieństwo że wylosowana kartą jest as kier? pierwsze losowanie (odkładanie 5 kart): A− odłożono 5 kart wśród których nie ma as kier B − odłożono 5 kart, jedną z nich jest as kier C− za drugim razem wycięto asa kier z 47 pozostałych kart Licz.

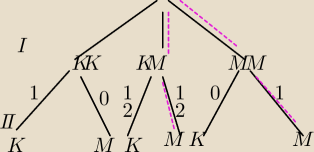
Mila: Z grupy 20 mężczyzn i 30 kobiet losujemy dwie osoby a następnie z tych dwóch osób wybieramy również w sposób losowy jedną. Jakie jest prawdopodobieństwo że wybierzemy mężczyznę? I losowanie

	30 2
P(KK)=
	50 2

	20 2
P(MM)=
	50 2

	20 1   30 1   *
P(KM)=
	50 2

A− wybrano mężczyznę w drugim losowaniu.

	20 2		20 1   30 1   *		1
P(A)=		*1+		*
	50 2		50 2		2

Hugo: a) 52−5 = 47 47/52 * 1/47 b) ∅? Bo nie da sie wylosowac odłożonej karty c) nie rozumiem iż wyciągnięto 5 kart i nie było tam tego asa i potem nie wylosowano go znowu? 47/52 * ..... ? = 0? I teraz bym rozumiał że zachodzi P(A) = P(A/a) P(a) + P(A/b) * P(b) + P(A/c) * P(c) = 47/52 * 1/47 ~ 1,92% i tu fajnie wychodzi poprzez 3 przypadki prawd. całkowite. Mówiłaś ze te przykłady nie dokońca oddają charakter tego więc opuściłem pozostałem podpunkty ale ok

Hugo: Już analizuję !

Mila: To zostaw na razie karty.Rozwiążemy, gdy będziesz miał trochę teorii na lekcji.

Hugo: Przeanalizowałem i nie jest to takie dokonca logiczne dla mnie lecz bardziej regułkowe mowa o ost linijce; Uwzględniamy dwa przypadki eliminując 3(KK) i nie podstawiając do wzoru (to czaje) chodziarz można podstawić i chyba by wyszło zero ;>? tam mamy (lub) czyli dodawanie x + y + 0 = x + y Jednak w drugim dodawaniu MM do KM mamy P(KM) i mamy to razy 1/2 hmmm zatem rozdzielamy to na równo (na pół) ? kobiet jest więcej więc jak mamy 1/2 z tego to w myślach roi mi się idea że wciąż mogą być wylosowane w mniejszym prawdopodobieństwie 2 kobiety z tego? . ... ; > O ile rozumiesz mnie bo ich jest więcej a dzielimy to na dwa{ P(KM)*1/2} Nie w pełni mój tok rozumowania rozumie twójzapis, jeżeli rozumiesz mnie prosze pomóż zrozumieć lepiej : ) Jeżeli poprostu tak jest bo 2+2=4 a nie 5 to rzecz do wyuczenia : )

Hugo: Skoro taka jest twa wola Zatem zawieszenie broni na dziś czy po moich 3 kawach robimy coś jeszcze ? Z chęcią porobię // wklepie przykład

Mila: Jeśli wylosowałeś kobietę i mężczyznę ( środkowa linia drzewka) to prawdopodobieństwo wyboru ze

	1
zbioru dwuelementowego mężczyzny jest		.
	2

Mila: Wróć do poprzednich zadań. (wczorajszych)

Hugo: aaaaaaaaaaa xD faceci 20 => 2 kobiety 30 => 2 I tu 2 i 2 to 50% .. OK rozumiem! dziękuję ! brałem wersje że 20 mężczyzn i 30 kobiet i tu razy 1/2... glupi ja. Zatem wracamy do wczorajszych.

Hugo: 12. Z talii 52 kart losujemy dwie karty. Oblicz prawdopodobieństwo że obie będą pikami jeśli obie nie są kierami ODP: 2/18 13. Ze zbioru liczb {1,2,3,4,5,6,7,8,9} losujemy dwie. Jakie jest prawdopodobieństwo że iloczyn tych liczb będzie nie parzysty, jeśli ich suma jest podzielna przez 3? ODP 1/3 14. Ze zbioru liczb trzy cyfrowych losujemy jedną liczbę. jakie jest prawdopodobieństwo że jest to liczba parzysta jeżeli wiadomo ze jest ona podzielna przez 25? 15. Rzucamy trzy razy kostką do gry. W drugim rzucie wypadła szóstka. Oblicz prawdopodobieństwo tego że suma oczek otrzymanych w trzech rzutach jest większa od 13 ODP 5/22 16. Rzucamy pięć razy kostką do gry. trzy razy otrzymaliśmy szóstkę. Oblicz prawdopodobieństwo tego ze w drugim rzucie otrzymaliśmy szóstkę. ODP 3/5

Mila: Popatrz na poprzedni wpis, tam masz rozwiązania niektórych.

Hugo:

	2 52
Ω =		// chyba że kolejność sie liczy...

A− obie są pikami i nie sa kierami B) obie nie są kierami

	2 13
P(A u B) =		/Ω // nie będzie tu wariacji bz powtórzeń ; / ?

	2 39
P(B) =		/Ω

	2 13		2 39
P(A/B) =		/		= 78/741

Hugo: 12*

Hugo: Odpowiedź to 2/18 mi wychodzi 2/19 ...

Hugo: PRZEPRASZAM 2/19 ! dobrze

Mila: Źle piszesz symbol Newtona

	13 2
Ma być.		itp.

Mila: Ma być iloczyn zbiorów . godz.21:40

Hugo: 13. Ze zbioru liczb {1,2,3,4,5,6,7,8,9} losujemy dwie. Jakie jest prawdopodobieństwo że iloczyn tych liczb będzie nie parzysty, jeśli ich suma jest podzielna przez 3? Ω = V 2 z 9 = 72 A − iloczyn parzysty i suma podzielna przez 3 B − suma podzielny przez 3 aby iloczyn był parzysty trzeba parzystą razy parzystą bądź parzysta razy nie parzysta / 2 przypadki? |Parzyste| = 4 |Nieparzyste| = 6 |Iloczyn parzystych| = V 2 z 2 n V 2 z 10 /// dla parzystych i dla parzysto nie parzystych |Iloczyn parzystych| = {2,4,6,8,10,12,14,16,18,24,20,28,32,36,30,40,42, 48, 54, 56,72} |Iloczyn parzystych| = 21 |Iloczyn parzystych| i podzielnych ich suma przez 3 ={12,15,18,24,36,30,42,48,54,72} |Iloczyn parzystych| = 9 (możliwe ze coś sie machłem) P(AuB) = 9/Ω P(B) = {12,15,18,24,21,27,36,42,45,51,54,63,72,81}/Ω = 14/Ω P(A/B) = 9/14 coś nie wychodzi...

Hugo: racja zapomniałem że N {}{} to właśnie to a nie symbolik z C gdzie zapisuje się na odwrót. Drugie postu troszke nie rozumiem... Więc zrobiłem teraz to ale coś nie wychodzi w odpowiedziach mam 1/4.. ale z pewnością coś się machłem pewnie z wyliczaniem odp możliwości. O tej porze nic nie wskóram dz ponownie coś mi powychodziło na szczęście Jak pani znajdzie błąd tu a wiem że gdzieś jest to prosze wskazać sb dokończę.. Miłej nocy odezwę się niebawem

Mila: W 13 wypisałam Ci zdarzenia i wynik jest U{1}[4}. Iloczyn ma być nieparzysty, suma podzielna przez 3 tam masz wypisane, dlaczego nie czytasz rozwiązań? wyjaśnień? Czytaj poprzedni post. (wczorajszy)