objętość stożka jest równa 144p{3} π cm^3, a pole jego podstawy ma 72π cm^2. Obl Karola: objętość stożka jest równa 144√3 π cm³, a pole jego podstawy ma 72π cm². Oblicz pole powierzchni całkowitej tego stożka.

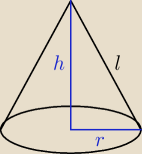
Michał: Z objętości i pola podstawy obliczysz wysokość stożka przekształcając wzór na objętość stożka. Z pola podstawy stożka, która jest kołem, wylicz jego promień przekształcając wzór na pole koła. Mając wysokość stożka i promień jego podstawy i traktując je, jako przyprostokątne i korzystając z tw. Pitagorasa, oblicz przeciwprostokątną, która pełni tu rolę tzw. tworzącej stożka. Znając dł. tworzącej stożka i promień jego podstawy oblicz powierzchnię boczną stożka: Pb = πrl. Dodaj do pola podstaw i po robocie. Pozdrawiam: sokol@owski.pl ( GG: 165 055 )

Karola: tylko że u mnie nikt nie rozumie tego zadania

dero2005: dane:

	πr2*h		Pp*h
V =		=		= 144√3π
	3		3

P_p = πr² = 72π wartość z drugej linijki wstawiamy do pierwszego wzoru

	72π*h
V =		= 144√3π |*3
	3

72π*h = 432√3π liczymy wysokość h

	432√3π
h =		= 6√3
	72π

ze wzoru na pole podstawy liczymy promień r r = √Ppπ = √72ππ = √72 = 6√2 z twierdzenia Pitagorasa liczymy tworzącą l l2 = r2 + h2 = (6√2)2 + (6√3)2 = 72 + 108 = 180 l = √180 = 6√5 liczymy pole pow bocznej Pb = πrl = π*6√2*6√5 = π36√10 liczymy pow całkowitą Pc = Pp + Pb = 72π + 36π√10 = 36π(2+√10)