Trygonometria Adi: Trygonometria Czy może mi ktoś pomóc rozwiązać takie rówanie: cos¹₂α 2sinα=³₂₄

Eta: Napisz poprawnie,tak jak masz w podręczniku,bo nie wierzę,że tak jest zapisane to równanie !

Saizou : zapisz używając U (wielkie U, zamiast małego przy pisaniu ułamków )

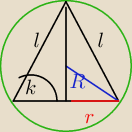
Adi: Dokładnie tak jak napisałem Tzn. robię zadnie ze stereometrii i po wszystkich podstawieniach wychodzi mi takie równianie. Szukam wzorów, kombinuję ale coś nie idzie. Sytuacja jak na rysunku. Szukamy kąta rozwarcia stożka Wiemy, ze stosunek pola powierzchni bocznej stożka do pola powierzchni kuli opisanej na tym stożku wynosi ³₈. cos1/2α=r/l, skorzystałem również ze wzoru R=l/2sinα

Adi: tu k=α

Adi: no chyba, że tego równania nie da się rozwiązać to jestem w kropce

Eta: Nie rysuj mi rysunku ! Napisz treść zadania! , to pogadamy

Adi: Stosunek pola powierzchni hocznej stożka do pola powierzchni kuli opisanej na tym stożku wynosi

	3
		. Znajdź kąt rozwarcia tego stożka.
	8

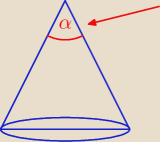
Eta: na rys. masz zaznaczony kąt rozwarcia stożka !

Adi: ojej, czyli w ogóle to nie ten kąt który zaznaczyłem

Adi: rzeczywiscie

Adi: twierdzenie sinusów tu zadziała?

Adi: jejciu, nie wiem jak to zrobić..mógłby mi ktoś pomóc?

Eta:

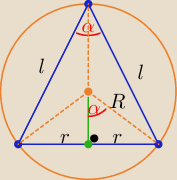
πrl		3		r
	=		⇒ 2rl=3R2 i		= sinα ⇒ r= R*sinα
4πR2		8		R

to: 2*R*l*sinα=3R² /:R

	3R
l=
	2sinα

z tw. cosinusów (2r)²=l²+l²−2*l*l*cosα (2Rsinα)²= 2l²(1−cosα)

	9R2
4R2sin2α= 2*		(1−cosα) /: R2
	4sin2α

	9
4sin2α=		(1−cosα) , /* sin2α≠0 , bo α∊(0,180o)
	2sin2α

8sin⁴α= 9−9cosα sin⁴α= (1−cos²α)² = 1−2cos²α+cos⁴α 8−16cos²α+8cos⁴α +9cosα−9=0 , cosα= t , t>0 i t≠1 8t⁴−16t²+9t−1=0 ...... otrzymasz

	1		3		√13		3		√13
t= 1 −− odrzucamy V t=		v t= −		+		v t=−		−		<0
	2		4		4		4		4

	1
cosα=		v cosα≈0,15
	2

α=60^o v α≈ 81^o Jaką masz odpowiedź ? ( sprawdzaj rachunki, bo być może się pomyliłam Chyba,że jest jeszcze inny sposób? cosα cosα

Eta: Te cosα........ niepotrzebnie mi się wpisały

Adi: Dziękuję. Zaraz będę analizować i dokładnie przeliczać. Mój matematyk niestety nie daje nam odpowiedzi, więc nawet nie mogę sprawdzić. Jeśli dostaniemy odpowiedź na lekcji to na pewno nie zapomnę jej tutaj zamieścić. Dziękuję jeszcze raz

Eta:

Eta: Rachunki nieco "koszmarne" ( dlatego pytałam o odpowiedzi)

Adi: Przyzwyczaiłem się również do "brzydkich" wyników, bo mój nauczyciel potrafi wymyślić dane na lekcji, ot tak − z kosmosu.. Czy jeśli byłabyś taka miła, mogłabyś podsunąć mi choć jakiś malutki pomysł do zadania którego niestety nie mogę ruszyć? Oto treść: W ostrosłupie prawidłowym czworokątnym płaszczyzna dwusieczna kąta między ścianą boczną i podstawą dzieli powierzchnię boczną ostrosłupa na dwie części o równych polach. Oblicz miarę kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Adi: Byłbym wdzięczny choć za małą wskazóweczkę, bo stereometria to chyba moja pięta achillesowa

Saizou :

πrl		3
	=
4πR2		8

rl		3
	=
4R2		8

	3
rl=		R2
	2

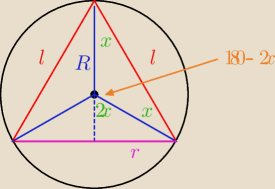
2rl=3R² z tw. sinusów mamy

l		R
	=
sin(180−2x)		sinx

l*sinx=R*sin(2x) l*sinx=2R*sinxcosx

	r
l=2R*cosx oraz cosx=
	l

	r
l=2R*
	l

	l2
r=
	2R

	l2
2l*		=3R2
	2R

l³=3R³ l=R√3 wstawiając do niebieskiego R√3=2R*cosx

	√3
cosx=		→x=30o
	2

to kąt rozwarcia to 2x=60^o tylko gdzie błąd skoro są 2 rozwiązania

Eta:

	r
Saizou czemu cosx=		?
	l

Adi: raczej sinx=^r_l

Saizou :

	r
tak sinx=		za bardzo chciałem sobie uprościć
	l

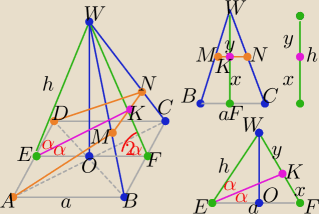
Eta: ADMN −−− płaszczyzna dwusieczna kąta 2α

	a   2		a
cos2α=		=		, 2α= ?
	h		2h

h −− dł. wysokości w ścianie bocznej , a−− dł. krawędzi podstawy |WF|= h=x+y ⇒ y= h−x , dla x<h

	x		y		ah
z tw. o dwusiecznej w trójkącie EFW :		=		........ ⇒ x=
	a		h		a+h

	ah
Pb= 4*		= 2ah to 0,5Pb= ah część pola bocznego ABMCND (oznaczam P2)
	2

P₂= ah

	a*x
i P(ΔABM)= P(ΔCDN)=
	2

	ah
P2= 2*P(ΔABM) +P(trapezuBCMN)= ax +		− P(ΔMNW)
	2

	y
Trójkąty MNW i BCW są podobne w skali k=
	h

	ah		y2		ay2		a(h−x)2
to: P(ΔMNW) = P(ΔBCW)*k2=		*		=		=
	2		h2		2h		2h

uwzględniając powyższe otrzymujemy: 0,5P_b= P₂

	ah		a(h−x)2
ah= ax+		−		/:a≠0
	2		2h

	h		h2−2hx+x2
h= x+		−		=0 /*2h
	2		2h

2h²= 2hx+h²−h²+2hx−x² x²−4hx+2h²=0 Δ_x= 8h² , √Δ_x= 2√2h x<h z założenia to przyjmujemy x= 2h−√2h =h(2−√2)

	ah
dla x= h(2−√2) i x=		(patrz ... wcześniej obliczone
	a+h

ah=(a+h)*h(2−√2) /:h

	a		2−√2
a= 2a−a√2+2h−h√2⇒ .....		=		= ..... = √2
	h		√2−1

	a		√2
to:		=
	2h		2

	a		√2
zatem cos2α=		=		⇒ 2α= 45o
	2h		2

A cóż za "sadystyczne " zadanie A może jest jakiś prostszy sposób, którego ja......... jak na razie nie widzę @ Adi ....... "pozdrów" ode mnie Twojego Pana za takie sadystyczne zadanie!

Adi: Ojej, dziękuję. Zaraz wszystko przeanalizuję. Twoja pomoc jest nieoceniona!

Eta: Myślę jeszcze, może jest jakiś prostszy sposób

AS: Moja propozycja rozwiązania

π*r*l		3
	=		=>
4*π*R2		8

8*r*l = 12**R62 −> 2*r*l = 3*R²

	2*r		r		l*sin(α/2)
r = l*sin(α/2) ,		= 2*R => R =		=
	sin(α)		sin(α)		2*sin(α/2)*cos(α/2)

	l
R =
	2*cos(α/2)

	l2
2*l*sin(α/2)*l = 3*
	4*cos2(α/2)

8*sin(α/2)*cos²(α/2) = 3 8*sin(α/2)*(1 − sin²(α/2)) = 3 8*sin³(α/2) − 8*sin(α/2) + 3 = 0 Rozwiązaniem tego równania jest sin(α/2) = 1/2 = 0.5 sin(α/2) = 1/4*(−1 − √13) = −1.1513 rozw.odpada sin(α/2) = 1/4*(√13 − 1) = 0.6514

Eta:

Adi: Mam jeszcze "fajne zadania". Jeśli ktoś chciałby pomóc to byłoby extra! 1. Na kuli o promieniu R opisano ostrosłup prawidłowy czworokątny, którego ściany boczne są nachylone do płaszczyzny podstawy pod kątem α. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa 2. Długość wysokości ostrosłupa prawidowego czworokątnego jest równa H. Kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę α. Oblicz objętość kuli opisanej na tym ostrosłupie. Dla jakicg wartości α zadanie ma rozwiązanie? 3. Długość wysokości stożka jest równa h, a tworząca jest nachylona do płaszczyzny pod kątem α. Płaszczyzna poprowadzona prostopadle do wysokosci dzieli powierzchmię całkowitą stożka na dwie części o równych polach. Oblicz wysokość otrzymanego stożka ściętego. 4. Oblicz objętość tego z ostrosłupów prawidłowych czwokątnych o krawędzibocznej dlugości l, w którym pole przekroju płaszczyzną zawierającą krawędź boczną i wysokość ostrosłupa jest największe. 5.Promień podstawt stożka jest równy r, a tworząca jest nachylona do podstawy pod kątem α. Przez wierzchołek stożka poprowadzono płaszczyznę tworzącą z osią stymetrii stożka kąt β. Oblicz pole przekroju 6. Przeciwprostokątna trójkąta prostokątnego ma długość 20 cm. Na jakie odcinki powinna podzielić przeciwprostokątna wyokość trójkąta, aby objętość bryły w wyniku obrotu tego trójkąta wokół przeciwprostokątnej była największa? Oblicz tę objętość

Adi: podbijam