Krawędź podstawy ostrosłupa prawidłowego czarnamagia: Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 2, a krawędź boczna 3{2}.Jakie możliwie najmniejsze pole ma przekrój tego ostrosłupa płaszczyzną zawierającą przekątną podstawy? odp.P={2}/3

irena_1: d=2√2

	d
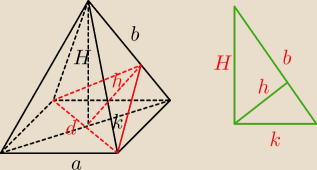
k=		=√2
	2

b=3√2 H²+(√2)²=(3√2)² H²=18−2=16 H=4 Przekrój jest trójkątem o podstawie 2√2 i wysokości h. W trójkącie prostokątnym o bokach H, k, b odcinek h jest odcinkiem łączącym wierzchołek kąta prostego z przeciwprostokątną. Najkrótszy taki odcinek to odcinek prostopadły do przeciwprostokątnej, czyli wysokość tego trójkąta opuszczona na przeciwprostokątną. Z pola tego trójkąta

4√2		3√2h
	=
2		2

	4
h=
	3

I najmniejsze pole przekroju:

	2√2*43		4√2
P=		=
	2		3

I nie zgadza mi się z odpowiedzią

czarnamagia: chyba źle przepisalam odp.Twoja jest dobra Wielkie dzięki