analiza iniektywność
PuRXUTM: mam spory problem
Sprawdź iniektywność funkcji f(x)=log
3 x
2
no więc jak weźmiemy x
1, x
2 ∊D
założymy że f(x1)=f(x2)
log
3 (x
1)
2=log
3 (x
2)
2
i jak 2 wrzucimy przed log to wychodzi że jest iniekcją a jak zostawimy to wychodzi że nie jest
Jak ten problem rozwiązać
2 lis 17:26
cze: logarytm jest różnowartościowy,
f(x) = log3 x2 = 2 log 3 x
2 lis 17:30
PuRXUTM: no ale jakbym liczył
log3 (x1)2 = log3 (x2)2
(x1)2=(x2)2
x1=x2 v x1=−x2...
2 lis 17:33
Trivial: Kontrprzykład: x = −3 oraz x = 3 dają takie same wartości.
2 lis 17:34
PuRXUTM: Trivial czyli co
nie jest iniekcją ?
2 lis 17:39
Mila:
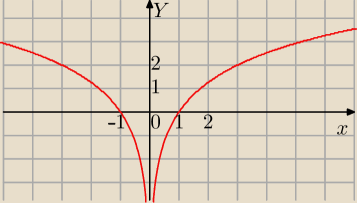
Funkcja log
3(x
2) nie jest różnowartościowa.
2 lis 17:44
PuRXUTM: dziękuje
2 lis 17:50
PuRXUTM: a mam pytanie jak mam 2 log
3 (x−1) to traktuje tak samo jak to wyżej
3 lis 11:29
PuRXUTM:
3 lis 11:54
wredulus_pospolitus:
tak
3 lis 11:55
PuRXUTM: strasznie to dziwne, a jak możesz narysuj mi wykres 2log3 x przecież to nie wychodzi to samo
co log3 x2...
2log3 x=y
log3 x=0.5y
30,5y=x
dla y=1 x=√3 a takiego punktu nie ma na wykresie log3 x2 ...
3 lis 12:09
Krzysiek: ten przykład już jest inny od log3x2
bo dla y=2log3x dziedzina jest inna niż dla y=log3x2
3 lis 13:13
PuRXUTM: ale przecież to to samo ... log
3 x
2=2log
3 x
3 lis 13:21
Krzysiek: jak już się ustali dziedzinę, bo przecież w piewszym przypadku x może być ujemne a w drugim już
nie.
3 lis 13:23
PuRXUTM: no ale to jest to samo czy nie, bo nie ogarniam....
3 lis 13:26
Krzysiek: nie. ustal dla jakich 'x' to jest równość
3 lis 13:27
PuRXUTM: dla x>0 ?
3 lis 13:28
Krzysiek: tak
3 lis 13:29
PuRXUTM: i wtedy wykresy się pokrywają
bo pewnie coś źle robię ale mi się nie pokrywają 12:09
3 lis 13:48
Krzysiek: tak, przecież ten punkt jest na wykresie
3 lis 13:52
PuRXUTM: ok dziękuje już rozumiem, nie zauważyłem tego
3 lis 13:53