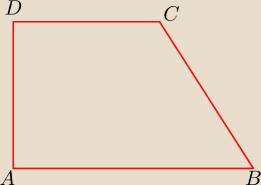
Sprawdzenie zadania Piotr 10: Dany jest trapez prostokątny o kącie prostym przy wierzchołkach A,D. Wyznacz współrzędne wierzchołka D trapezu ABCD, jeśli wiadomo, że A=(−2;1), B=(6;5) , C=(2;8). Wykaż, że kąt nachylenia prostej AB do osi OX jest mniejszy od 45⁰. Rozwiązanie:

	yB−yA		5−1		1
aAB=		=		=
	xB−xA		8		2

a_AB=a_DC

	1
aDC=
	2

y_DC=a_DC*x+b₁ 8=0,5*2+b₁ b₁=7 y_DC=0,5x+7 y_AD=a_AD+b₂ a_AD= − 2 (prosta AD jest prostopadła do prostej DC) y_AD=−2x+b₂ 1=−2*(−2)+b₂ b₂=5 y_AD=−2x+5 y_DC=0,5x+7 y_AD=−2x+5 0,5x+7=−2x+5 2,5x=−2 x_D= −0,8⇔y_D=6,6 D=(−0,8 ; 6,6) Prosta AB: y_AB=0,5x+b⇔1=0,5*(−2)+b⇔b=2⇔y_AB=0,5x+2 Kąt nachylenia prostej AB do osi OX to a=tgα tgα=0,5 α≈27⁰ < 45⁰ Proszę o sprawdzenie

Piotr 10:

Saizou :

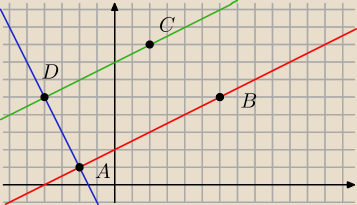
	1
− prosta AB l: y=		x+2
	2

− prosta prostopadła do AB przechodząca przez punkt A k: y=−2x−3

	1
− prosta prostopadła do prostej k przechodząca przez punkt C m: y=		x+7
	2

− punkt D to punkt przecięcia się prostych m oraz k ⇒D(−4:5)

	1		√3
tgα=		a wiemy że tg45=		, ponadto wykres funkcji tgx jest rosnący dla
	2		3

	π		π		1		√3
x∊(−		+kπ:		+kπ) zatem wystarczy pokazać że		<		co jest prawdą, zatem
	2		2		2		3

α<45^o czy jakoś tak