funkcje cyklometryczne Jout2: Ile wynosi arcsin(sin3) , arccos(sin3) oraz jak to policzyć bo nie rozumiem?

Jout2: f5

Mila: 1)

	π		π
arcsin(sin(3))=α i α∊<−		,		>
	2		2

	π
3>
	2

arcsin(sin(3))=arcsin(sin(π−3)),

	π		π
arcsin(sin(π−3))=π−3 (π−3)∊<−		,		>
	2		2

2) arccos(sin3) =α , α∊<0,π>

	π		π
sin3=cos(		−3)=cos(3−		) cos (x) jest funkcją parzystą,
	2		2

	π
(3−		)∊<0,π>
	2

	π		π
arccos(sin3) =arccos(cos(3−		)=3−
	2		2

Jout2:

	π
Kurcze nie za bardzo rozumiem skąd się bierze w a) akurat π−3 a w b)		−3
	2

Próbuję zrozumieć te funkcje z złożone z arcusami ale jakoś nie znalazłem dobrze wytłumaczonego materialu

Jout2: mógłby ktoś to wytłumaczyć mi?

Trivial: Przypominam definicję arcsin arcsin: [−1,1] → [−^π₂, ^π₂] Zatem mamy: arcsin(y) = x ⇔ y = sin(x) ∧ x ∊ [−^π₂, ^π₂] Czyli arcsin(sin(u)) = x ⇔ sin(u) = sin(x) ∧ x ∊ [−^π₂, ^π₂] Innymi słowy, x jest u sprowadzonym do przedziału [−^π₂, ^π₂] bez zmiany wartości funkcji sinus.

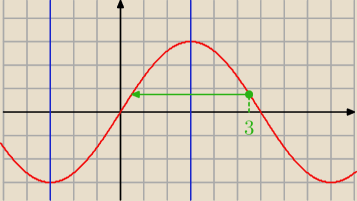
Trivial: Przykład a) narysowany. arcsin(sin(3)) = π−3

Jout2: Ja rozumiem, że chodzi tu o sprowadzenie do odpowiedniego przedziału tylko za bardzo nie wiem jak znaleźć odpowiednie π żeby to działało jak należy. A jak by wyglądało to dla arcsin(sin10) ?

Trivial: Można wymyślić procedurę postępowania. 1. Sprowadzamy u do przedziału [−π,π] poprzez dodanie 2kπ. Oznaczmy wynik przez x. 2. Jeżeli mamy x ∊ [−^π₂, ^π₂] to procedura zakończona. W przeciwnym razie jeśli x > 0 to wynikiem jest π−x jeśli x < 0 to wynikiem jest −(π+x)

Trivial: dla u = 10 mamy x = 10−4π ≈ −2.56 < −^π₂ wynikiem jest −(π+x) = −(π+10−4π) = 3π−10.

Jout2: Czyli sprawdzam odejmując od u wartosci 2kπ ? I powiedzmy 10 − 2kπ dla k=1 10−2π = 3,72 a to nie należy do przedzialu [−π,π] więc szukam dalej? wtedy trafiam dla k=2 na 4π co daje −2.56, które należy do przedzialu [−π,π] więc sprawdzam pkt 2 procedury. Tak to działa?

Trivial: Tak.

Jout2: Okey, a jak by było dla cosinusa? arccos(cos10) można użyć tej samej procedury, zmieniając w pkt 2. zakres [0, π] czy coś jeszcze trzeba zmienić?