Zadanie
gość: Wyznacz liczbę rozwiązań równania w zależności od wartości parametru m. W przypadku istnienia
rozwiązań wyznacz je.
|x+3| + |x+9| = m
tutaj link do częściowego rozwiązania zadania:
http://i40.tinypic.com/1gp3pj.jpg
30 paź 21:14
Godzio:
Rozwiązanie jest dobre. Jedynie wykres by się przydał, żeby było wiadomo, że ta m > 6 nie
wzięło się z kosmosu
30 paź 21:19
gość:

Czy to jest dobry wykres?
30 paź 21:30
Mila:
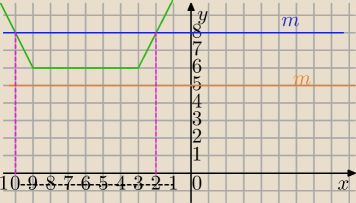
f(x)=|x+3| + |x+9|
1) |x+3|=x+3 ⇔x≥−3
|x+9|=x+9⇔x≥−9
2) |x+3|=−x−3 ⇔x<−3
|x+9|=−x−9 ⇔x<−9
rozważymy wzór f(x) w przedziałach: (−
∞,−9)∪<−9,−3)∪<−3,
∞)
a) x∊(−
∞,−9)
f(x)=−x−3−x−9⇔f(x)=−2x−12
b) x∊<−9,−3)
f(x)=−x−3+x+9=6 funkcja stała
c) x∊<−3,
∞)
f(x)=x+3+x+9=2x+12
m<6 brak rozwiązań
m=6 nieskończenie wiele rozwiązań:
x∊<−9,−3>
m>6 dwa rozwiazania
x<−9 i m>6 mamy równanie :
−2x−12=m
−2x=m+12
| | −m−12 | | −8−12 | |
x= |
| (np.dla m=8 to x= |
| =−10) |
| | 2 | | 2 | |
x>−3 i m>6 mamy rownanie:
2x+12 =m
2x=m−12
| | m−12 | | 8−12 | |
x= |
| (np. dla m=8 to x= |
| =−2) |
| | 2 | | 2 | |
30 paź 21:53
daras: m ≥ 6
30 paź 22:08
daras: czyli jak widać z wykresy rozwiązania są ja m≥6 jedno albo dwa

31 paź 16:11
 Czy to jest dobry wykres?
Czy to jest dobry wykres?
 f(x)=|x+3| + |x+9|
1) |x+3|=x+3 ⇔x≥−3
|x+9|=x+9⇔x≥−9
2) |x+3|=−x−3 ⇔x<−3
|x+9|=−x−9 ⇔x<−9
rozważymy wzór f(x) w przedziałach: (−∞,−9)∪<−9,−3)∪<−3,∞)
a) x∊(−∞,−9)
f(x)=−x−3−x−9⇔f(x)=−2x−12
b) x∊<−9,−3)
f(x)=−x−3+x+9=6 funkcja stała
c) x∊<−3,∞)
f(x)=x+3+x+9=2x+12
m<6 brak rozwiązań
m=6 nieskończenie wiele rozwiązań: x∊<−9,−3>
m>6 dwa rozwiazania
x<−9 i m>6 mamy równanie :
−2x−12=m
−2x=m+12
f(x)=|x+3| + |x+9|
1) |x+3|=x+3 ⇔x≥−3
|x+9|=x+9⇔x≥−9
2) |x+3|=−x−3 ⇔x<−3
|x+9|=−x−9 ⇔x<−9
rozważymy wzór f(x) w przedziałach: (−∞,−9)∪<−9,−3)∪<−3,∞)
a) x∊(−∞,−9)
f(x)=−x−3−x−9⇔f(x)=−2x−12
b) x∊<−9,−3)
f(x)=−x−3+x+9=6 funkcja stała
c) x∊<−3,∞)
f(x)=x+3+x+9=2x+12
m<6 brak rozwiązań
m=6 nieskończenie wiele rozwiązań: x∊<−9,−3>
m>6 dwa rozwiazania
x<−9 i m>6 mamy równanie :
−2x−12=m
−2x=m+12
