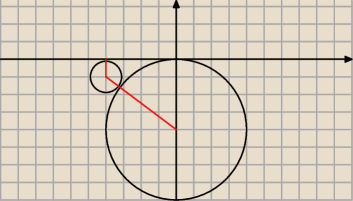
 Wsp. środka tego okręgu, to (0,−4), jego promień r=4
Szukamy wsp. xs i ys środków okręgów stycznych do OX i zadanego okręgu.
Okręgi styczne do OX mają promień równy |ys|
Jeżeli okręgi są styczne, to odległość pomiędzy ich środkami jest równa sumie ich promieni
Mamy więc:
(xs−0)2+(ys−(−4))2=(|ys|+4)2 −−− wziąłem kwadraty odległości
Po wymnożeniu:
xs2+8ys=8|ys|
Dla ys≥0 nie ma rozwiązań, bo wychodzi nam xs=ys=0, czyli okrąg zdegenerowany do punktu
Dla ys<0 dostajemy:
Wsp. środka tego okręgu, to (0,−4), jego promień r=4
Szukamy wsp. xs i ys środków okręgów stycznych do OX i zadanego okręgu.
Okręgi styczne do OX mają promień równy |ys|
Jeżeli okręgi są styczne, to odległość pomiędzy ich środkami jest równa sumie ich promieni
Mamy więc:
(xs−0)2+(ys−(−4))2=(|ys|+4)2 −−− wziąłem kwadraty odległości
Po wymnożeniu:
xs2+8ys=8|ys|
Dla ys≥0 nie ma rozwiązań, bo wychodzi nam xs=ys=0, czyli okrąg zdegenerowany do punktu
Dla ys<0 dostajemy:
| 1 | ||
xs2+8ys=−8ys ⇒ ys=− | xs2 | |
| 16 |