Funkcja kwadratowa bezendu: Funkcja kwadratowa f określona jest wzorem f(x)=(3m−5)x²−(2m−1)x+0,25(3m−5) Wyznacz te wartości parametru m∊R, dla których najmniejsza wartość jest liczba dodatnią 3m−5>0 Δ<0 Takie warunki?

Piotr 10:

	Δ
q=−
	4a

czyli Δ < 0 jest ok

Piotr 10: Może weź jeszcze zbadaj gdy 3m−5=0

bezendu: Czemu ?

Piotr 10: Zawsze się powinno sprawdzić co się będzie działo gdy będzie to funkcja liniowa. Nie wiem czy w

	5
tym zadaniu trzeba. Ale podstaw za m=		i powiedz co wychodzi
	3

Eta: f(x)=ax²+bx+c osiąga minimum , gdy a>0 i y_w>0

Piotr 10: Eta czyli nie trzeba warunku sprawdzać gdy 3m−5=0

Eta: Nie... bo funkcja liniowa nie ma wartości najmniejszej !

bezendu: Eta ramiona będą skierowane w górę, brak miejsc zerowych, więc y_w>0 dobrze myślę ?

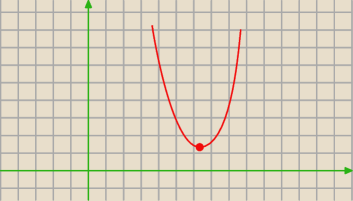
bezendu: skoro Δ<0 i a>0 to wierzchołek jest na osią OX

Eta:

	−Δ
a>0 i yW=q=		>0 ⇒ Δ<0
	4a

czyli dobrze myślisz

Eta:

bezendu: Czyli dobrze, że upierałem się przy swoim ! A podobnież już wszystkie rozdane na forum

Eta: Jedno "robaczywe".... jeszcze zostało

bezendu: Wykaż, że jeśli funkcje f(x)=x²+px+q i g(x)=x²+qx+p gdzie p≠q, mają wspólne miejsca zerowe to p+q=−1

Piotr 10: Hahah co za przypadek, też patrzyłem na te zadanie dziś A.Kiełbasa

bezendu: Dokładnie

Piotr 10:

x1+x2
	= xw
2

Zacznij może od tego, ja to już lecę spać

Eta:

	p−q
x2+px+q=x2+qx+p ⇒ x=		= 1 dla p≠q
	p−q

to: f(1) =0 ⇒1+ p+q=0 ⇒ p+q=... g(1)=0 ⇒ ........

bezendu:

	p−q
x=
	p−q

Eta: px−qx= p−q ⇒ x(p−q)= p−q ⇒ x=.....

bezendu: p+q=−1 g(1)=1+q+p p+q=−1

Eta: No i c.n.u

bezendu: Dziękuję i życzę szybkiego powrotu do zdrowia

Eta: