wielomian
Radek:
Wielomian T(x) jest wynikiem dzielenia wielomianu W(x)=2x
3−2x
2−5x+2 przez dwumian x−2. Zapisz
wielomian T(x) jako iloczyn dwóch wielomianów pierwszego stopnia
Po podzieleniu wielomianu W(x) przez dwumian x−2 mam
T(x)=(x−2)(2x
2+2x−1)
Δ=12
√Δ=2
√3
| | −2−2√3 | | 2(−1−√3 | | −1−√3 | |
x1= |
| = |
| = |
| |
| | 4 | | 4 | | 2 | |
| | −2+2√3 | | 2(−1+√3 | | −1+√3 | |
x2= |
| = |
| = |
| |
| | 4 | | 4 | | 2 | |
ale tu nie wyjdzie iloczyn dwóch lecz trzech wielomianów
29 paź 19:17
Beti: dwumian (x−2) nie jest częścią wielomianu T(x)
29 paź 19:19
Hajtowy: (x−2)(x+x
1)(x+x
2)
Chyba o taką formę chodzi

29 paź 19:19
Radek:
Beti czyli jak to zapisać i jak pozmieniać znaki w tych nawiasach ?
29 paź 19:22
Radek: up
29 paź 20:03
Saizou :
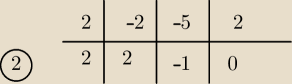
T(x)=2x
2+2x−1=....
29 paź 20:18
Radek:
| | −1−√3 | |
Nie chodzi o to jak mam x= |
| ta jak to zapisać w postaci iloczynowej |
| | 2 | |
(x−jak zmienić poszczególne znaki)
29 paź 20:21
Saizou : a jak masz np. x1=−2 i x2=3 to jak byś to zapisał ?
29 paź 20:23
Radek:
| | −1−√3 | |
(x+2)(x−3) ale tu mam problem |
| |
| | 2 | |
29 paź 21:04
29 paź 21:06
Radek: czyli znaki zmieniasz przy 1 i √3
29 paź 21:13
Saizou : tak bo tego minusa sprzed ułamka wciągnąłem do licznika
29 paź 21:18

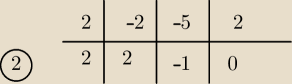 T(x)=2x2+2x−1=....
T(x)=2x2+2x−1=....