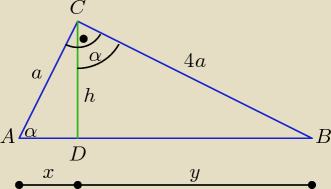
 Zadanie z testów maturalnych.
Trójkąty ADC, BDC, ABC są podobne.
Mamy wykazać, że y = 16x.
Zadanie z testów maturalnych.
Trójkąty ADC, BDC, ABC są podobne.
Mamy wykazać, że y = 16x.
| x | a | a2 | ||||
Z podobieństwa trójkątów ADC i ABC: | = | ⇒ x + y = | ||||
| a | x + y | x |
| y | 4a | 16a2 | ||||
Z podobieństwa trójkątów BDC i ABC: | = | ⇒ x + y = | ||||
| 4a | x + y | y |
| a2 | 16a2 | 1 | 16 | |||||
A więc | = | / : a2 ⇒ | = | ⇒ y = 16x. | ||||
| x | y | x | y |
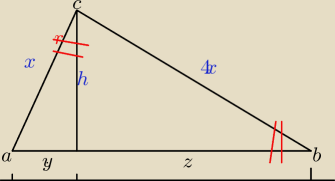
| x*x4 | ||
PΔabc = | =2x2 | |
| 2 |
| x√17*h | |
=2x2 | |
| 2 |
| √17 | x | ||
= | |||
| 4 | h |
| 4x | √17 | ||
= | |||
| z | 4 |
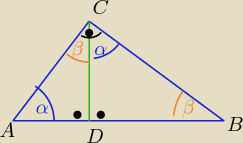 α+β= 90o
Czy teraz jasne?
α+β= 90o
Czy teraz jasne? 
| x | ||
cosα= | ||
| a |
| y | ||
sinα= | ||
| 4a |
| sinα | y | a | ||||
tgα= | = | * | ||||
| cosα | 4a | x |
| y | ||
tgα= | ||
| 4x |
| 4a | ||
tgα = | = 4 | |
| a |
| y | ||
4 = | ||
| 4x |