Proszę o pomoc Paula: Oblicz objętość i pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego wiedząc, że krawędź jego podstawy ma długość 4 √2 cm, a krawędź boczna ma długość 5 cm.

wredulus_pospolitus: a jakiej pomocy od nas byś oczekiwała ?

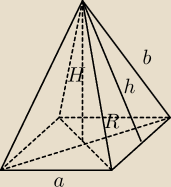
irena_1: a=4√2cm b=5cm h²+(2√2)²=5² h²=25−8=17 h=√17

	1
Pb=4*		*4√2*√17=8√34cm2
	2

	1		1
R=		a√2=		*4√2*√2=4cm
	2		2

H²+R²=b² H²=5²−4²=25−16=9 H=3cm P_p=(4√2)²=32cm²

	1
V=		*32*3=32cm3
	3

gtt: https://matematykaszkolna.pl/strona/995.gif po pierwsze znaj podstawy jak on wygląda i zo możesz z nim robić.

	1
V=		Pp *H
	3

Pb=suma pól trójkątów podstawa− a=4√2 Pp= a² =(4√2)²=32 H=? k=5 k krawędź boczna d− przekątna podstawy = a√2 = 4√2 *√2=4*2=8 z trójkąta prostokątnego A²+B²=C²

	1		1
mamy k2=d2+H2 ====> H2=k2−(		d)2 ===> H2=52−(		*8)2=25−16=9
	2		2

H²=9 / √

	1
H=3 do wzorku na V =		*32*3=32
	3

	a*h
stąd H=3, a=4√2 h− wysokość trójkąta Pb =4*		=
	2

h= ponownie trójkąt prostokątny tym razem wysokość trójkąta=h, H oraz a

	1
h2=(		a)2+H2
	2

	1
h2=(		*4√2)2 + 32 ===>8*9=72
	2

h²=72 / √ h=√72=√36*2=6√2

	a*h		4√2*6√2
Pb =4*		= 4*		=96
	2		2

jeśli się pomyliłem poprawcie mnie

Paula: wiec ktore jest dobrze