2 zadania optymalizacyjne kaś: 1. Z prostokątnego arkusza tektury o wymiarach 20cm x 30cm wycieto w rogach kwadraty o boku dlugosci x. Po zgięciu zbudowano prostopadłościenne otwarte pudełko: a)Wyznacz wzór funkcji opisujacej pole pow. bocznej tego pudełka w zaleznosci od dlugosci boku wycietego kwadratu, podaj dziedzine tej funkcji b)Dla jakiej długości x pole pow. bocznej pudelka jest najwieksze z mozliwych? Wyznacz to pole. 2.Suma długości podstawy trójkąta i wysokości opuszczonej na tę podstawę wynosi 30cm. Wyznacz długość tej podstawy i wysokość tak, aby pole trójkąta było najwieksze. Bardzo proszę o pomoc.

dan: a) P_b(x)= −8x²+ 100X D_f : x∊(0 , 10)

dan: b) dla x=⁵⁰₈ P_b (⁵⁰₈)=

dan: chyba coś nie tak ⁵⁰₈ poza dziedziną

dan: co ja pisze w dziedzinie

dan: powinno być ok

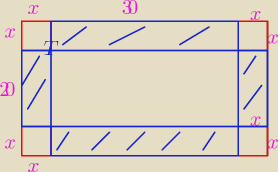
dan: Ten zakreskowny granatowy obszar to pole boczne. Wystarczy ułozyć równanie które jest wyżej

kaś: dziękuję bardzo, już rozumiem

wiki: trójkąt równo boczny ABC ma obwodrowny 18cm. jakądługoś ma każdy bok trójkata

Mmmmmm: ale dlaczego dziedzina w zad 1 a x∊(o , 10 ) ?