Rozwiąż algebraicznie następujący układ równań Mati: Rozwiąż algebraicznie następujący układ równań:

⎧	x−|y−4|=4
⎩	|x−3|+|y−4|=3

irena_1: Narysuj proste o równaniach x=3 oraz y=4. Podzielą płaszczyznę na 4 części. I. Dla x≥3 i y≥4 masz układ x−(y−4)=4 x−3+y+4=3 i rozwiązanie x=5 y=5 II. Dla x<3 i y≥4 masz układ x−(y−4)=4 −x+3+y−4=3 Jest to układ sprzeczny Φ III. Dla x<3 i y<4 masz układ x−(4−y)=4 3−x+4−y=3 Układ sprzeczny Φ IV. Dla x≥3 i y<4 masz układ x−(4−y)=4 x−3+4−y=3 I rozwiązanie x=5 y=3 Masz więc pary: (5, 5), (5, 3)

Mati: Na 4 części? Nie wiem jakie i dlaczego w ogóle jest raz ≥ raz > ?

Aga1.: Ix−3I=x−3, gdy x−3≥0, czyli x≥3 Ix−3I=−(x−3), gdy x−3<0, czyli x<3 Podobnie rozpisz Iy−4I i rozpatrujesz 4 przypadki (kolejność nie ma znaczenia) 1)x≥3 i y≥4 2) x≥3 i y<4 3) x<3 i y≥4 4) x<3 i y<4

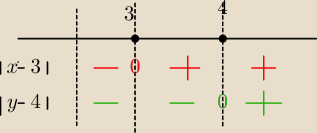
krystek: Ix−3I i Iy−4I i musisz rozpatrzyć m zerowe to 3 i 4 i przeczytaj uważnie co napisała Irena