równanie okręgu bla bla: dany jest okrąg x²+y²−2x−4y−11=0 i prosta l o równaniu x−y−3=0. Wyznacz równaie okręgu symetrycznego do danego wzgledem l

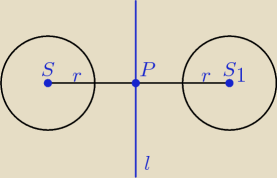
AROB: Z danego równania okręgu wyznaczamy jego środek i promień. x² + y² −2ax − 2by + c = 0 Z przyrównania: −2a = −2 ⇒ a = 1 c+ −11 −2b = −4 ⇒ b = 2 , czyli S(1,2) r = √a²+b²−c = √1+4+11 = 4 − Wyznaczamy równanie prostej SP⊥ l l: x−y−3 = 0 ⇒ y = x − 3

	1
al = 1, aSP = −		= −1
	al

SP : y − y_s = a_SP(x − x_S) y − 2 = − (x − 1) ⇒ y = −x + 3 − Wyznaczamy punkt P z przecięcia prostych l i SP: y= −x + 3 y = x − 3 ⇒ x−3 = −x+3 ⇒ x = 3 y = 0, czyli P(3,0) − Wyznaczamy punkt S₁ ( P jest środkiem odcinka SS₁ ):

	xS + xS1		yS + yS1
xP =		yP =
	2		2

	1 + xS1		2 + yS1
3 =		0 =
	2		2

1 + x_S1 = 5 2 + yS₁ = 0 x_S1 = 5 y_S1 = −2 S₁(5, −2) r = 4 Zatem równanie okręgu symetrycznego ma postać: (x−a)² + (y − b)² = r² (x − 5)² + (y + 2)² = 16

Kasia: A jak wyznaczyć z tego początkowego równania r i S?

Klaudia: na jakiej zasadzie sie wyznacza wzor prostej prostopadlej? Wiem ze ze wzoru bedzie a = −1 wiec: y = −x + b A skad jest y = −x + 3 Nie rozumiem jak wyiczyc to b

Klaudia: ?