średnie Saizou : Eto masz jakieś zadanka na dowodzenie za pomocą nierówności o średnich, bo chyba się zmobilizowałem żeby to jakoś ogarnąć może dzisiaj tylko do 23 ale zawsze coś

Eta: Może jutro Dzisiaj jestem kontuzjowana ( zerwałam ścięgno w nodze

Saizou : uuu.... a co się stało? za dużo jabłek zbierałaś na zimę ?

Mila: Eto, szybkiej regeneracji ścięgna życzę. Miałam coś takiego w klasie maturalnej, strasznie mnie bolało, ale tylko jedną noc, potem przeszło.

PW: W zastępstwie. Znajdź najmniejszą dodatnią wartość funkcji

	2x2+3
f(x) =
	x

Eta: Dzięki Mila Myślałam,że to już koniec z bólu dwa razy zemdlałam ( echhh ta "młodość'

Eta:

	2√6
odp do zad. PW
	3

zgadza się ?

PW: Nie.

Saizou : a mi wyszło że 2√6

PW: Dobrze, ale bardzo ważne jest uzasadnienie, nie sama nierówność między średnimi (może niepotrzebnie o tym piszę, ale trzeba sprawdzić, kiedy ma miejsce równość).

Eta: No mi też 2√6

Saizou : znaczy się ja policzyłem pochodną

	3		√6		√6
f'(x)=2−		=0 ⇒x=		lub x=−		nas interesuje tylko dodatnie
	x2		2		2

	√6
f(		)=....=2√6
	2

pigor: ...np. tak :

	1
y=		i x≠0 ⇔ yx= 2x2+3 ⇔ 2x2−yx+3=0 , to Δ ≥0 ⇔
	2x2+3

⇔ y²−24 ≥ 0 ⇔ y² ≥ 4*6 ⇔ |y| ≥ 2√6 i y>0 ⇔ y ≥ 2√6, stąd y= 2√6 − szukana wartość najmniejsza y . ...

Gustlik: Eta, życzę szybkiego powrotu do zdrowia Na pocieszenie .

pigor: ... , o kurcze, widziałem tylko zadanie, a nie Ciebie Eta − cierpiącą, ale teraz − mocno zawstydzony − życzę tego i wszystkiego co w tej chwili pozwoli Tobie czuć się co najmniej tak, jak przed nieszczęsnym zerwaniem ...

pigor: ...., wracając do zadania z godziny 01:24 podaję inny sposób (nie z nierówności między średnimi a−g) rozwiązania zadania :

	2x2+3
znajdź najmniejszą dodatnią wartość funkcji f(x)=		; przepraszam , ale
	x

	1
nie mam pojęcia skąd wziął mi się tam taki zapis wzoru y=		, skoro dalej
	2x2+3

	2x2+3
po znaku ⇔ rozwiązuję dla wzoru f(x)=		.... Ufff , może to ta noc, itd. itp.
	x

dlatego moje takie dwie kolejne wpadki

pigor: ...no to jak już chyba ... "obudziłem się" i aby już zamknąć moje gadu, gadu :

	2x2+3
f(x)=		= 2x+3x ≥ 2√2x*3x = 2√6
	x

przy czym najmniejszą, dodatnią wartość f(x)= 2√6 funkcja osiąga dla x>0 takiego, że 2x= ³_x ⇔ 2x²=3 ⇔ √2|x|=√3 ⇒ 2x= √6 ⇔ x= ¹₂√6 . ...

PW: O, to to, pigor, właśnie takie sprawdzenie sugerowałem Saizou. Nie można skończyć na nierówności wynikającej z twierdzenia o średnich, daje ono w tym wypadku tylko oszacowanie z dołu. Osiąganie przez funkcję wartości 2√6 wymaga sprawdzenia, czy

	3
jest spełniony warunek x1=x2, w tym wypadku 2x=		. Łatwo byłoby złośliwie tak narzucić
	x

ograniczenia na x, że funkcja tej wartości 2√6 nie osiągnie.

Saizou : Eto jak zdrówko?

Saizou : jakbyś miała chęci to możesz wrzucić jakieś zadanko na średnie ?

Mila: Eta pewnie źle się czuje. dla poprawy samopoczucia.

Eta: Musisz jeszcze poczekać ze dwa dni ( bo musiałabym znaleźć zadania w swoim archiwum a nie mogę jeszcze chodzić o własnych siłach

Eta: Dzięki Mila za wsparcie

Saizou : spokojnie, ważniejsze jest zdrowie

daras: @ PW f(x)_min = 2√6 > 0, to wynika z badania przebiegu zmienności funkcji: dla x = 0 jest asymptota pionowa a dla x < 0 funkcja jest ujemna, natomiast dla x>0 ma wartości dodatnie przy czym pierwsza pochodna ma miejsce zerowe się dla x = ^√6₂, a druga pochodna f''(x=^√6₂) > 0 ⇒minimum.

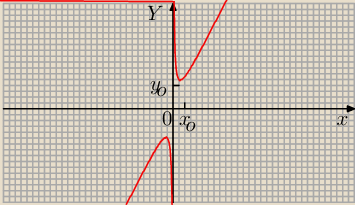
daras: x_o = ^√6₂, y_o = 2√6

Mila:

Mila: Eto, jakie postępy w leczeniu? Jest ulga?

Eta: Echh niestety ...ale jeszcze nie ma ulgi, jestem na środkach przeciwbólowych Ważne,że żyję

Mila: Wszystko, przejdzie, byłam 4 tygodnie na środkach przeciwbólowych, zapalenie nerwu żebrowego. Też myślałam,że to koniec ze mną, dopóki nie postawiono diagnozy. Spokojnej nocy.

PW: @daras, to co piszesz o badaniu funkcji jest prawdą, ale zaczęło się od pytania Saizou o zadanie na zastosowanie twierdzenia o nierówności między średnimi. Dałem zadanie, które jest właśnie niebanalnym zastosowaniem tego twierdzenia. Bez znajomości rachunku różniczkowego można znaleźć ekstremum, co pokazał pigor wczoraj o 9:36. Dowcip polega na tym, że badanie funkcji jest czasochłonne, a tu − dwie linijki, rozumowanie prościutkie.

daras: Lubię różniczki i mi to też zajęło 2 linijki nie licząc wykresu i słowotoku

Saizou : Eto masz już tyle sił żeby się ze mną 'użerać', czy jeszcze poczekać zresztą jak tam zdrówko?

Godzio: Może ja dam jakieś zadanko ?

Saizou : mam się bać

Godzio: Nie ma czego Zad. 1 Wykaż, że dla x,y,z ≥ 0

	x + y + z		x		y		z
		≤		+		+
	1 + x2 + y2 + z2		1 + x2		1 + y2		1 + z2

Zad 2 Wykaż, że jeśli a + b = 1 to

	1
a4 + b4 ≥
	8

Saizou : zad. 2

	a4+b2		a+b
4√		≥
	2		2

a4+b4		1
	≥
2		2*2*2*2

	1
a4+b4≥
	8

Godzio: Za łatwe

Saizou : ale zad 1 już nie takie łatwe

PW: Ale też chyba i "za łatwo" rozwiązane.

Godzio: Zad. 3 Niech a i b będą liczbami rzeczywistymi. Udowodnij, ze jeśli ax² − ax − b < 0 dla każdego rzeczywistego x, to również x² + 3 + 3a²b|x| > 3³√2x² dla x ∊ R

Godzio: PW co masz na myśli ? Brak komentarza czy pominięcie jednego kroku pomiędzy

	a4 + b4		a + b
4√		≥		?
	2		2

Saizou : myślę, myślę i nic nie przychodzi mi na myśl na razie

Godzio: Myśl, myśl

Saizou : nie mam pomysłu, może przez noc coś wymyślę, a teraz lecę, także do usłyszenia

PW: @Godzio, ja wiem, że Saizou to wszytko rozumie, ale jak "na sprzedaż", to brak mi właśnie przywołania twierdzenia i tego pośredniego kroku. Czytelnik, który nie wie tego samego (czyli nie zna rozwiązania) nie jest w stanie zrozumieć skąd się to wzięło.

Godzio: Uznałem, że już aż taki szczegółowy nie musi być Wierze, że na maturze będzie wszystko opisywał aż za nadto Pamiętam jak ja rozwiązywałem zadania i z czegoś korzystałem to jeszcze dla wszystkiego to udowadniałem, żeby nie było się do czego przyczepić

PW: A dowód zadania 1. jest "szokująco prosty", ale trzeba przyznać, że zadanie na pierwszy rzut oka onieśmiela, dowcipne.

Eta: @ [N[Saizou] ........nie leń się .......... do pracy! Zad1/ Wykaż,że tg13^o+tg27^o+tg33^o+tg43^o+tg47^o+tg57^o+tg63^o+tg77^o >8 Zad2/ Wykaż,że dla x,y,z >0 i x, y, z≠1 zachodzi:

	logxz*logyz
logxyz=
	logxz+logyz

Zad3/ Wykaż,że dla a, b, c€ R+ (a²+b²+c²)(a+b+c) ≥ 9abc powodzenia

Saizou : cały czas myślę, ale jakoś nie mogę wymyślić

Eta: Eta... mmm

Godzio: Mam nadzieję, że cały czas o moim myślisz

Eta:

Eta: zad1/ oczywiście, bez użycia tablic i kalkulatora

Saizou : tak Godzio i jakoś nie mogę przestać

Eta: No to napisz rozwiązania do moich zadań ( skoro tylko myślisz nad Godziowymi

Saizou : nie czepiać się słówek późno jest myślę globalnie, ale jak widać jestem jeszcze za słaby ta takie zadanka ale trzeba ćwiczyć

Eta:

Saizou : w 3 zadanku mam moment że (a+b+c)(ab+ac+bc)≥3abc i na razie nie wiem co dalej

Saizou : tam maiło być (a+b+c)(ab+ac+bc)≥9abc i teraz tak myślę żeby pokazać że a²+b²+c²≥ab+ac+bc

Eta: dwa razy ......am −gm

Saizou : czyli że jak, bo nie łapię

Eta:

a2+b2+c2
	≥3√a2*b2*c2
3

a+b+c
	≥3√abc
3

pomnożyć stronami i jest teza

Saizou : jakie to było banalne , a ja tego nie wymyśliłem

Eta: No przecież chciałeś ze średnimi! Zad1/ też banalne ! ...... sam ....

Saizou : nie wyprę się tego, bo kiedyś trzeba to ogarnąć

Eta: Dawaj zad1/ (2 sekundy) i jest teza

Godzio: Dłuuuuuuuuugie 2 sekundy

Saizou : zad. 2

	1		1		1		1
tg13+		+tg27+		+tg33+		+tg43+		>8
	tg13		tg27		tg33		tg43

gm−hm

	1		1		1		1
8√tg13*		*tg27*		*tg33*		*tg43*		=1
	tg13		tg27		tg33		tg43

	8		1		1		1		1
1≥		+		+tg27+		+tg33+		+tg43+
	tg13		tg13		tg27		tg33		tg43

	1		1		1		1
tg13+		+tg27+		+tg33+		+tg43+		≥8
	tg13		tg27		tg33		tg43

tg13+tg27+tg33+tg43+tg47+tg57+tg63+tg77 ≥8 coś takiego ?

Saizou : oczywiście miało być

	8
1≥
	1   1   1   1   tg13+ +tg27+ +tg33+ +tg43+   tg13   tg27   tg33   tg43

Eta: z nierówności między średnimi am−gm

tg13+tg27+ .....
	> 8√tg13*tg27.. = 1 bo tg13*tg77= tg13*ctg13=1 itp
8

Saizou : a czy tak jak ja zrobiłem jest dobrze ?

Eta:

	1
Mogłeś wstawić "lemat" a+		≥2
	a

	1
w tym przypadku : tg13+		>2
	tg13

	1
tg27+		>2
	tg63

: : + =================== dodać stronami i masz tezę

Eta: Równość nie zajdzie !

Saizou : to tak jest zawsze dla a>0

Eta: W drugim mianowniku oczywiście, że ma być tg27

Eta: No tak, założenie zostawiłam Tobie i ....

Saizou : będzie na szarlotkę