zad new: dany jest trojkat rownoboczny ABC Punkty P Q R leza na bokach trojkata ABC (po jednym na kazdym boku)w taki sposob ze kazdy bok Trojkata PQR jest prostopadly do jego boku a)wykaz ze trojkat PQR jest rownoboczny b)wyznacz stosunek IARI −−−−−− IPQI

new: nie umie nikt?

new: odswiezam

new:

new:

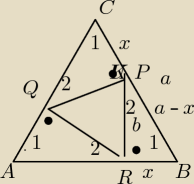
AS: Kąt 1 = 60^o , kąt 2 = 30^o Trójkąty RBP , PQC i AQR są podobne bo mają odpowiednie kąty równe. Wobec tego RB = PC = AQ = x są równe.

x		1
	= cos60o =		⇒ 2*x = a − x ⇒ 3*x = a ⇒ x = a/3
a−x		2

PR		a		√3		a*√3
	= tg(1) ⇒ b = x*tg(60o) =		*		=
RB		3		3		9

	PQ		QR
Podobnie		= tg(1) oraz		= tg(1)
	PC		AQ

co świadczy że boki PR , PQ i QR są równe,są więc bokami trójkąta równobocznego.

	a2*√3
Pole trójkąta danego P1 =
	4

	b2*√3		(a*√3		√3
Pole trójkąta wpisanego P2 =		=		)2}*		}
	4		9		4

AS: Dokończenie zadania Zagalopowałem się − pole trójkąta jest niepotrzebne.

|AR|		a − x
	=		= (a − 2a/3)/(a*√3/9) = (a/3)*(9/a√3) =
|PQ|		b

18		2
	=
9√3		√3

new: dzieki AS