wielomian misia: Wyznacz dziedzinę funkcji i naszkicuj wykres funkcji f(m) = x₁² +x₂², gdzie x₁ i x₂ są różnymi pierwiastkami równania x² − mx = −m² + 2m − 1 To zadanie już się gdzieś pojawiło i widziałam tam podpowiedź, której nie zrozumiałam. Czy mógłby mi ktoś pomóc rozwiązać to zadanie?

irena_1: x²−mx+(m−1)²=0 Δ=m²−4(m−1)²=(m−2(m−1))(m+2(m−1))=(−m+2)(3m−2)>0

	2
m∊(		; 2)
	3

	2
Df=(		; 2)
	3

f(m)=x₁²+x₂²=(x₁+x₂)²−2x₁x₂=(−m)²−2(m−1)²=m²−2m²+4m−2=−m²+4m−2

Basia: x² − mx + (m²−2m+1) = 0 Δ>0 (bo masz mieć dwa różne pierwiastki) Δ = m² − 4*1(m²−2m+1) = m² − 4m³ + 8m − 4 = −3m² + 8m − 4 −3m² + 8m − 4 > 0 /*(−1) 3m² − 8m + 4 < 0 Δ_m = 64 − 4*3*4 = 64−48 = 16

	8−4		4		2
m1 =		=		=
	6		6		3

	8+4
m2 =		= 2
	6

m∊(²₃; 2) i to jest dziedzina funkcji f(m) f(m) = x₁²+x₂² = (x₁+x₂)² − 2x₁*x₂ z wzorów Viete'a

	−b		c
f(m) = (		)2 − 2*
	a		a

	−(−m)		m2−2m+1
f(m) = (		)2 − 2*
	1		1

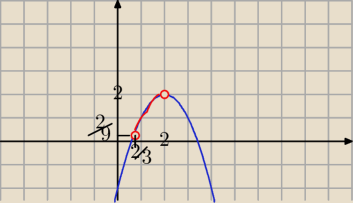
f(m) = m² − 2m² + 4m − 2 f(m) = −m² + 4m − 2 = −(m²−4m) − 2 = −[ (m−2)² − 4 ] − 2 = −(m−2)² + 2 parabola ramiona w dół; wierzchołek W(2;2) i szkicujesz fragment paraboli w dziedzinie podanej wyżej

	4		8		−4+24−18		2
f(2/3) = −		+		− 2 =		=
	9		3		9		9

więc to jest mniej więcej ten czerwony kawałek