zbiór liczb zespolonych
q: zbiór liczb zespolonych spelniajacych rownanie:
| z + i | + | z − i | = 2
prosze o jakiekolwiek wskazowki; z gory serdecznie dziekuje
27 paź 19:01
Basia: dopiero co było; Mila bardzo dokładnie opisała rozwiązanie
szukaj
27 paź 19:08
Godzio:
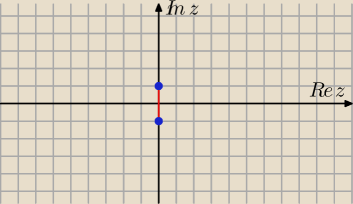
Suma odległości od punktu (0,i) i (0,−i) jest równa 2
Re(z) = 0 i Imz ∊ [−1,1]
27 paź 19:11
q: ok, dziekuje; jeszcze tylko to, tez nie wiem jak ruszyc:
oznaczenia: z sprzezone zapisze tak: ~z
|~z + 2 − i| <= |z|
27 paź 19:22
Godzio:
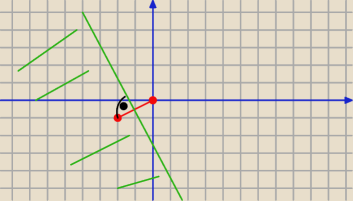
|~z| = |z|
|~z + 2 − i| = |z + 2 + i| ≤ |z|
To jest ten obszar który zaznaczyłem, geometrycznie jest to obszar pod symetralną odcinka
składającego się z tych dwóch punktów: (−2,−i) i (0,0)
27 paź 19:33
q: ponownie dziekuje za pomoc; interpretacje geometryczna rozumiem, tylko nadal nie czaje, jak
wyprowadziles:
|~z + 2 − i| = |z + 2 + i|, korzystajac z tego, ze |~z| = |z|
czy ma to powiazanie z symetria wzgledem osi Re?
27 paź 19:41
q: ok, juz wiem; napisze dla kompletnosci:
|~z + 2 − i| = |~(~z + 2 − i)| = |z + 2 + i|
27 paź 20:03
Mila:
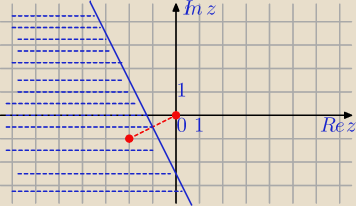
Jesli nie 'widzisz', tej prostej (tu symetralnej) to rozpisujesz:
z=x+iy, x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i(−y−1)|≤x+iy|⇔
√(x+2)2+(y+1)2|≤
√x2+y2 /
2
x
2+4x+4+y
2+2y+1≤x
2+y
2
4x+5+2y≤0
| | 5 | | 5 | |
y≤−2x− |
| punkty poniżej prostej y=−2x− |
| |
| | 2 | | 2 | |
27 paź 20:23
 Suma odległości od punktu (0,i) i (0,−i) jest równa 2
Re(z) = 0 i Imz ∊ [−1,1]
Suma odległości od punktu (0,i) i (0,−i) jest równa 2
Re(z) = 0 i Imz ∊ [−1,1]
 |~z| = |z|
|~z + 2 − i| = |z + 2 + i| ≤ |z|
To jest ten obszar który zaznaczyłem, geometrycznie jest to obszar pod symetralną odcinka
składającego się z tych dwóch punktów: (−2,−i) i (0,0)
|~z| = |z|
|~z + 2 − i| = |z + 2 + i| ≤ |z|
To jest ten obszar który zaznaczyłem, geometrycznie jest to obszar pod symetralną odcinka
składającego się z tych dwóch punktów: (−2,−i) i (0,0)
 Jesli nie 'widzisz', tej prostej (tu symetralnej) to rozpisujesz:
z=x+iy, x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i(−y−1)|≤x+iy|⇔
√(x+2)2+(y+1)2|≤√x2+y2 /2
x2+4x+4+y2+2y+1≤x2+y2
4x+5+2y≤0
Jesli nie 'widzisz', tej prostej (tu symetralnej) to rozpisujesz:
z=x+iy, x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i(−y−1)|≤x+iy|⇔
√(x+2)2+(y+1)2|≤√x2+y2 /2
x2+4x+4+y2+2y+1≤x2+y2
4x+5+2y≤0