Ostrosłupy immfine : W ostrosłupie trójkątnym ściany boczne są nachylone do płaszczyzny podstawy podstawy pod tym samym kątem. Wykaż, że spodek wysokości ostrosłupa jest środkiem okręgu wpisanego w podstawę tego ostrosłupa. Prosze o rozwiązanie z rysunkiem. Z góry dziękuję.

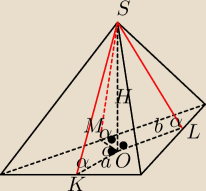
irena_1: Masz 3 trójkąty prostokątne o wspólnej przyprostokątnej H leżącej naprzeciw tych kątów w trójkątach. a, b, c to odległości spodka wysokości od boków wielokąta podstawy.

	H		H		H
ctgα=		=		=
	a		b		c

Musi być więc a=b=c, czyli spodek wysokości jest równo odległy od wszystkich boków podstawy. Jest więc środkiem okręgu wpisanego w podstawę.