rozwiąż równanie
Wiesiu: |3x2+2x|=x|3x+2|
czy mogę wyciągnąć x przed wartość bezwzględną?
x|3x+2|=x|3x+2|
6 paź 17:52
AS: nie,jedynie w obrębie wartości bezwzględnej,ustalić miejsca zerowe
i zbadać w jakim przedziale przyjmuje wartości dodatnie a w jakim ujemne.
6 paź 17:55
new: As poradzis zco sna moje zadania?
6 paź 18:00
Wiesiu: Jak wyznaczyć dobrze przedział?
np. w pierwszym przypadku
10 20
3x2+2x≥0 3x+2≥0
x1= −2/3 x≥−2/3
x2= 0
x∊(jaki to przedział)
6 paź 18:03
Wiesiu: sorry bez tej 20
6 paź 18:05
Wiesiu: czy to będzie x∊<o,+∞>
6 paź 18:30
Wiesiu: x∊<0,+∞)
6 paź 18:32
RunMan: Jak dla mnie x∊<0;∞) ∪ {−23}
6 paź 19:05
RunMan: w sensie, że podałem rozwiązanie
A tak poza tym, to przyrównujesz każdą wartość bezwzględną do 0, wyznaczasz miejsca zerowe
funkcji zarówno kwadratowych i liniowych. Następnie zapisujesz każdy z przedziałów (nawias
domknięty tam, gdzie funkcja przyjmuje wartość dodatnią). Potem badasz jak zachowuje się
wartość bezwzględna, gdy x należy do danego przedziału − gdy wychodzi wartość ujemna,
opuszczasz wartość bezwzględną z minusem, a następnie otrzymany wynik przyrównujesz do zakresu
który badałeś. Jeżeli otrzymana liczba / zakres należy do badanego zakresu, wtedy otrzymujesz
rozwiązanie.
Uważaj na domknięcia nawiasów − łatwo się pomylić.
6 paź 19:09
AS:
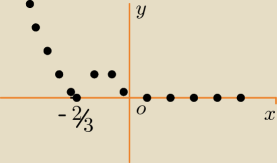
|3*x
2 + 2*x| = x*|3*x + 2|
|x*(3*x + 2)| − x*|3*x + 2| = 0
|x|*|3*x + 2| − x*|3*x + 2| = 0 |3*x + 2| przed nawias
|3*x + 2|*(|x| − x|) = 0
Miejsce zerowe |3*x + 2| wynosi −2/3 , a |x| − 0 (zero)
Rozpatruję przedziały (−
∞,−2/3) , −2/3 , (−2/3,0) , 0 , (0,
∞)
Dla x ∊ (−
∞,−2/3) np. −2 |3*x + 2| = −(3*x + 2) , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
−(3*x + 2)*(−2*x) = 2*x*(3*x + 2) = 6*x
2 + 4*x (lewa strona wykresu)
Dla x = −2/3 |3*x + 2| = |3*(−2/3) + 2| = 0 , |x| − x = |−2/3| − (−2/3) = 2/3 + 2/3 = 4/3
czyli lewa strona równania ma postać
0*(4/3) = 0
Dla x ∊ (−2/3,0) np. −1/3 |3*x + 2| = 3*x + 2 , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
(3*x + 2)*(−2*x) = −6*x
2 − 4*x (środkowa część wykresu)
Dla x ∊ (0,
∞) np. 10 |3*x + 2| = 3*x + 2 , )x| − x = x − x = 0
czyli lewa strona równania ma postać
(3*x + 2)*0 = 0 (prawa atrona wykresu)
6 paź 19:11
Wiesiu: dzięki
6 paź 19:19
ala: 2−3x
−−−−−−−=−1/2=

?
1−2x
13 kwi 17:05
ala: jak to się robiło
13 kwi 17:06
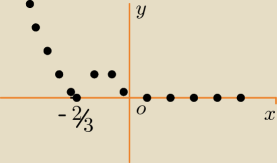 |3*x2 + 2*x| = x*|3*x + 2|
|x*(3*x + 2)| − x*|3*x + 2| = 0
|x|*|3*x + 2| − x*|3*x + 2| = 0 |3*x + 2| przed nawias
|3*x + 2|*(|x| − x|) = 0
Miejsce zerowe |3*x + 2| wynosi −2/3 , a |x| − 0 (zero)
Rozpatruję przedziały (−∞,−2/3) , −2/3 , (−2/3,0) , 0 , (0,∞)
Dla x ∊ (−∞,−2/3) np. −2 |3*x + 2| = −(3*x + 2) , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
−(3*x + 2)*(−2*x) = 2*x*(3*x + 2) = 6*x2 + 4*x (lewa strona wykresu)
Dla x = −2/3 |3*x + 2| = |3*(−2/3) + 2| = 0 , |x| − x = |−2/3| − (−2/3) = 2/3 + 2/3 = 4/3
czyli lewa strona równania ma postać
0*(4/3) = 0
Dla x ∊ (−2/3,0) np. −1/3 |3*x + 2| = 3*x + 2 , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
(3*x + 2)*(−2*x) = −6*x2 − 4*x (środkowa część wykresu)
Dla x ∊ (0,∞) np. 10 |3*x + 2| = 3*x + 2 , )x| − x = x − x = 0
czyli lewa strona równania ma postać
(3*x + 2)*0 = 0 (prawa atrona wykresu)
|3*x2 + 2*x| = x*|3*x + 2|
|x*(3*x + 2)| − x*|3*x + 2| = 0
|x|*|3*x + 2| − x*|3*x + 2| = 0 |3*x + 2| przed nawias
|3*x + 2|*(|x| − x|) = 0
Miejsce zerowe |3*x + 2| wynosi −2/3 , a |x| − 0 (zero)
Rozpatruję przedziały (−∞,−2/3) , −2/3 , (−2/3,0) , 0 , (0,∞)
Dla x ∊ (−∞,−2/3) np. −2 |3*x + 2| = −(3*x + 2) , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
−(3*x + 2)*(−2*x) = 2*x*(3*x + 2) = 6*x2 + 4*x (lewa strona wykresu)
Dla x = −2/3 |3*x + 2| = |3*(−2/3) + 2| = 0 , |x| − x = |−2/3| − (−2/3) = 2/3 + 2/3 = 4/3
czyli lewa strona równania ma postać
0*(4/3) = 0
Dla x ∊ (−2/3,0) np. −1/3 |3*x + 2| = 3*x + 2 , )x| − x = −x − x = −2*x
czyli lewa strona równania ma postać
(3*x + 2)*(−2*x) = −6*x2 − 4*x (środkowa część wykresu)
Dla x ∊ (0,∞) np. 10 |3*x + 2| = 3*x + 2 , )x| − x = x − x = 0
czyli lewa strona równania ma postać
(3*x + 2)*0 = 0 (prawa atrona wykresu)
 ?
1−2x
?
1−2x