Udowodnij twierdzenie.
zerker:
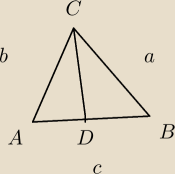
|CD| jest dwusieczną kąta C. Udowodnij twierdzenie, że: |AD| : |DB|=b : a.
27 paź 10:34
Piotr 10: Najlepiej chyba z twierdzenia sinusów.
27 paź 10:37
zerker: Nadal nie mam pomysłu. Dzieląc kąt C na 2 co do czego możemy porównać?
27 paź 10:46
Piotr 10:
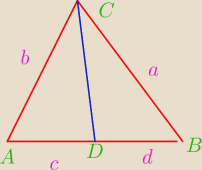
ΔADC
ΔDCB
| d | | a | | d | | a | |
| = |
| = |
| = |
| |
| sinβ | | sin(180−α) | | sinβ | | sinα | |
| c | | b*sinβ | | sinα | | b | |
| = |
| * |
| = |
| |
| d | | sinα | | a*sinβ | | a | |
27 paź 10:47
Piotr 10: I<ADCI=α
I<BDCI=180−α
I<DCAI=β
I<DCBI=β
27 paź 10:48
Piotr 10: Kurde trochę źle to rozpisałem(chaotycznie), ale mam nadzieję ,że wiesz o co chodzi
27 paź 10:50
zerker: Tak już się domyśliłem, wielkie dzięki.
27 paź 10:55
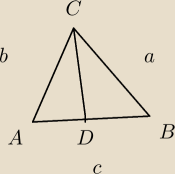 |CD| jest dwusieczną kąta C. Udowodnij twierdzenie, że: |AD| : |DB|=b : a.
|CD| jest dwusieczną kąta C. Udowodnij twierdzenie, że: |AD| : |DB|=b : a.
 ΔADC
ΔADC