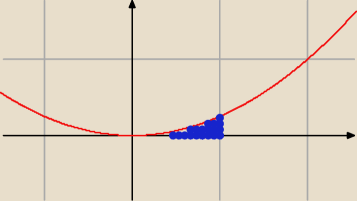
. asdf: Witam, prawdopodobienstwo: Z odcinka <0,1> wybieramy losowo dwie liczby: p i q. Jakie jest prawdopodobienstwo, ze rownanie x² + px + q = 0 ma dwa różne pierwiastki? Ω = <0,1> x <0,1> = kwadrat

	p2
P(A) = Δ > 0 ⇒ p2 − 4q > 0 ⇒ q <
	4

	p2		p3		1
w takim razie będzie to ∫01		dp =		| 10 =		− 0 =
	4		12		12

	1
	12

tak?

Trivial: Wygląda OK.

asdf: dzieki

asdf: Dany jest rozkład: x_i || 3 || 4 || 5 || 9 p_i ||0.1||0.1 || 0.2|| 0.6 Obliczyć P(√X ≤ 2) z dziedziny: X ≥ 0, czyli: P(√X ≤ 2) = P( 0 ≤ √X ≤ 2) = P(0 ≤ X ≤ 4) = F(4+0) − F(0) = 0.2 ok?

asdf: chodzi mi o warunek z zerem, bo jeżeli miałbym atom x_k = −4, to F(0) i tak będzie sumował dla p_k, w takim przypadku nalezy odrzucić te rozwiązania dla F(0) < 0? (tak jak zrobiłem), czy sam warunek: P(√X ≤ 2) = P(X ≤ 4) [bez ograniczenia z dołu]

Trivial: Przecież F(0) = 0. Poza tym ja nie wiem co kombinujesz. Można przecież napisać: P[√X ≤ 2] = P[X ≤ 4] = 0.1 + 0.1 = 0.2

asdf: wiem, że F(0) = 0, ale jakbym miał przypadek dla F(0) ≠ 0 to przedział wyglądałby z ograniczeniem z dołu czy nie?

Trivial: Dobre pytanie. Nie wiem.

asdf:

asdf: Mam takie zadanie: Wyznaczyc stałą k, aby funkcja F(x) była dystrybuantą zmiennej losowej X typu ciągłego. F(x) = { 0 dla x ≤ 2

	5
{ 4(1 −		) dla 2 ≤ x ≤ k
	x

{ 1 dla x > k dalej mam napisane:

	20
Funkcja gęstości dla takiej dystrybuanty ma postać f(x) = F'(x) =
	x2

skąd to się bierze?

asdf: chyba już wiem... można to zrobić tak?: dystrybuanta to całka dla funkcji gęstości, czyli pole te musi byc 1: F(x) = _−∞∫^x f(x) dx = 1

	5		1		−20
F'(x) = f(x) ⇒ f(x) = (4(1−		) )' = 4* (−5) *		=
	x		x2		x2

więc:

	−20		20
∫2k (		dx = −		+ 10
	x2		k

Pole = 1, więc:

	20
−		+ 10= 1
	k

	20
−		= −9
	k

20
	= 9
k

	20
k =
	9

to jest ok?

asdf: ?

Krzysiek: F'(x)=20/x² i musisz rozpisywać wszystko dla jakich 'x' F'(x)=20/x² również ∫_−∞^∞f(x)=1 czyli ∫_−∞^∞f(x)=∫_−∞²f(x)dx+∫₂^kf(x)dx+∫_k^∞f(x)dx=0+∫₂^kf(x)dx+0

Krzysiek: poza tym,że F'(x)=20/x² to dalej dobrze liczyłeś z tego co widzę.

asdf: A no tak Znak inny (pochodnych sie dawno nie liczyło ) Dzięki bardzo