. Piotr 10: Z punktu P=(−2;0) poprowadzono styczne do okręgu x²+y²+4y+3=0. Znajdź równania tych stycznych i oblicz sinus kąta ostrego, jakie one tworzą. Wychodzą mi tutaj brzydkie liczby trochę: x²+(y+2)²=1 S=(0;−2) y=a(x+2)+0 ax−y+2a=0 równanie prostej stycznej do okręgu

	−4−√7		−4+√7
a=		v a=
	3		3

I nie wiem czy dobrze to zrobiłem. Później jeszcze ten sinx muszę policzyć a mając takie ''a'' to będzie trochę ciężko w liczeniu tego

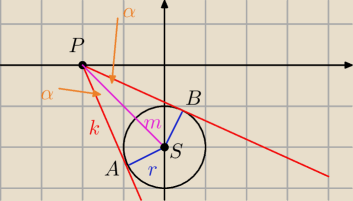
Saizou : m=2√2 r=1 k²+1=8 k=√7

	1		√7
PAPS=P{BPS}=		*√7*1=
	2		2

1		√7
	*√7*2√2*sinα=
2		2

2√2*sinα=1

	1		√2
sinα=		=
	2√2		4

sin2α=2sinαcosα doliczamy cosinus mając wiedzę że 2α∊(0:90)

	√2
(		)2+cos2α=1
	4

1
	+cos2α=1
8

	7
cos2α=
	8

	√14
cosα=		bo α∊(0:90)
	4

	√2		√14		√7
sin2α=2*		*		=
	4		4		4

jak czegoś nie pomyliłem

Piotr 10: A dobrze mam tamto wyliczone, co wcześniej napisałem

MQ: Muszę cię zmartwić −− mi tak samo wyszło, niestety.

MQ: Oczywiście, pisałem o wyliczeniu "a".

Piotr 10: Bo chciałem ten wzór zastosować https://matematykaszkolna.pl/strona/1228.html wyliczyć tgx potem z jedynki trygonometrycznej. Ale przy takim ''a'' tym wzorem to nie za bardzo chyba

Saizou : jak dla mnie

Piotr 10: A jak myślicie, tym wzorem co podałem link wcześniej jakoś by dało radę czy nie za bardzo ?

Saizou : pewno by dało, ale jak sam napisałeś, rachunki mogą być nieprzyjemne

Saizou : a masz odp. to tego zadanka?

Piotr 10: Ok. Dzięki Wam za pomoc

Piotr 10: Właśnie nie mam odpowiedzi, mam arkusze maturalne od pani ze szkoły i powiedziała, że nie ma też do nich odpowiedzi, więc tutaj piszę jak mi jakieś ''marne'' liczby wychodzą

MQ: Wcale nie takie trudne −− bardzo ładnie się redukują niewymierności.

Saizou : MQ użyłem trybu przypuszczającego i chyba dobrze wyliczyłem, znaczy się wyniki zgadzają mi się z geogebrą

Mila: Wg oznaczeń na rysunku Saizou |PS|=2√2, |SB|=1, PB²=(2√2)²−1² |PB|²=7⇔|PB|=√7 w ΔSBP:

	SB		1
sinα=		=
	PS		2√2

	PB		√7
cosα=		=
	PS		2√2

	1		√7		√7
2sinα*cosα=2*		*		=		=sin(2α)
	2√2		2√2		4

Saizou : można było skorzystać z funkcji trygonometrycznych dla trójkąta prostokątnego, a nie z jedynki trygonometrycznej, w sumie na jedno wychodzi ale chyba łatwiej z trójkąta

MQ:

	√7
Mnie ze wzoru na tg różnicy kątów wyszło tg2α=
	3

α −− jak w Waszych oznaczeniach.