Szufladki maciej: Trivial, Mila, inni Możecie pomóc mi przy tym zadaniu? W krainie Nibylandii jest jeden z lepszych pisarzy − Profesor Z. W ostatnich dniach wydał książkę, której napisanie zajęło mu 81h w przeciągu 10 dni. Udowodnij, że w okresie pisania ksiązki były dwa kolejne dni w ciągu których profesor spędził co najmniej 17h nad tekstem. Wskazówka była taka, aby skorzystać z metody szufladkowej, lecz nie wiem od czego się zabrać, a tym bardziej jak to zapisać formalnie.

Mila: Przy założeniu, że w każdym dniu poświęcał pełną liczbę godzin na pisanie . 81h=10*8h+1h conajmniej w jednym dniu profesor musiał spędzic 9h na pisaniu. 9h+8h=17h Zobaczymy co na to Trivial

Trivial: Trivial nic na to. Tak samo bym zrobił.

MQ: Mila udowodniła tylko, że istnieje taki dzień, w którym pracował 9h. Żeby udowodnić tezę, trzeba podzielić czas nie na 10 dni (szufladek) tylko na 5 par dni (szufladek).

Trivial: MQ, słuszna uwaga.

maciej: czyli 10 * 8h = 5 * (2 * 8h) + 1h ?

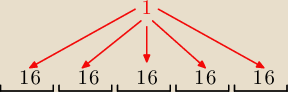
Trivial: Przy innym rozkładzie godzin niż "po równo" od razu mamy sytuację, że gdzieś jest 17 godzin. Przy rozkładzie równym (po 16 wszędzie) zostaje nam jedna godzina. Dokładamy ją do dowolnej szufladki i mamy 17 godzin.

MQ: Raczej nie: 10*8h=80h 5*(2*8h)+1h=81h 80h≠81h

Trivial: * przynajmniej 17 godzin.

MQ: To raczej nie było oczywiście do 19:58. Trivial już ci wytłumaczył o 20:05.

PW: Par dni jest 9: (1,2), (2,3), (3,4),..., (9, 10)

maciej: tak, wyżej zapomniałem (10 * 8h ) + 1h = [...] natomiast mam jeszcze jedno zadanie: Na szachownicy (8x8) możemy rozpatrzyć taką zabawę, że: na pierwszym jej polu kładziemy jedno ciasteczko, na drugim − dwa ciasteczka, na trzecim − cztery ciasteczka, na czwartym − osiem ciasteczek, aż do wypełnienia każdego pola. Zadanie: a) podaj zależność rekurencyjną zwracającą ilość ciasteczek na zadanym polu b) rozwiąż tę metodę za pomocą funkcji generujących Pierwsze co zauważyłem to wzór ogólny:

⎧	a1 = 1
⎩	an = 2*an−1

Jeżeli się mylę to proszę poprawcie mnie , i jak zrobić b) ?

Trivial: PW, to bez znaczenia. Wystarczy że twierdzenie działa dla par "rozłącznych": (1,2), (3,4), ..., (9,10)

MQ: @PW nie mieszaj! Dzielimy czas na pięć okresów dwudniowych i udowadniamy, że w przynajmniej jednym z nich pracował 17h.

MQ:

	10 2
Tak, nawiasem mówiąc, par dni jest

Trivial: MQ... Kolejnych par tyle nie ma.

maciej: jakis pomysł odnośnie tego zadania drugiego?

MQ: @Trivial −− dlatego

MQ: maciej punkt a) dobrze Co do b), to się nie wypowiadam, bo nie wiem co to funkcja generująca.

Krzysiek: maciej, a funkcja generująca to to samo co funkcja tworząca?

PW: @MQ − zadanie mówi o parach kolejnych dni, więc nie zbijaj mnie z tropu mówiąc, że par jest

	10 2
		. Taki głupi to ja nie jestem. Nie rozumiem natomiast, dlaczego uznajesz za kolejne

dni tylko (1,2), (3,4), (5,6), (7,8) i (9,10). A (8,9) to nie są kolejne dni?

maciej: Krzysiek właśnie nie jestem pewny, ponieważ tego jeszcze nie miałem

maciej: ale chyba o to chodzi http://pl.wikipedia.org/wiki/Funkcja_tworz%C4%85ca

MQ: @PW Napisałeś "par dni jest 9". NIE napisałeś "par dni kolejnych jest 9"

MQ: @PW Co do drugiej części Twoich uwag. Nam nie chodzi o wyliczenie ile jest par kolejnych dni, tylko o podzielenie okresu 10 dni na równe okresy dwudniowe −− jest ich 5.

Krzysiek: obstawiałbym za funkcjami tworzącymi, bo nimi się rozwiązuje równania rekurencyjne. f(x)=∑_n=0^∞a_n xⁿ=1/2+∑_n=1^∞a_n xⁿ=1/2+∑_n=1^∞2a_n−1xⁿ= =1/2+2x∑_n=0^∞a_n xⁿ f(x)=1/2+2xf(x)

	1/2		1
f(x)=		=(*)=		*∑n=0∞(2x)n=1/2∑n=0∞2n*xn
	1−2x		2

	1
(*)−korzystam z szeregu geometrycznego ∑n=0∞		=tn
	1−t

zatem a_n=1/2*2ⁿ=2ⁿ⁻¹ , n≥1

maciej:

	1
dlaczego tam masz w pierwszej linijce		+ suma ?
	2

Krzysiek: policzyłem pierwszy element sumy który wynosi a₀ , a a₀=1/2

maciej: mógłbyś napisać jak to się robi, ponieważ chyba zapomniałem

Trivial: Funkcje generujące do takiego zadania to jakieś nieporozumienie.

	an
an = 2an−1 →		= 2 → ciąg geometryczny.
	an−1

maciej: sztuka dla sztuki ?

Krzysiek: Trivial od jakiegoś przykładu trzeba zacząć, jak widać w tym przypadku od razu funkcję f(x) można rozwinąć w szereg. maciej, co konkretnie nie rozumiesz co napisałem? szukasz f(x) a potem musisz tą funkcję rozwinąć w szereg i patrzysz na to co stoi przy xⁿ

maciej: ok już rozumiem, może któryś z was rozumie grafy? ponieważ znalazłem ciekawe zadanie (przynajmniej dla mnie, bo zaczynam dopiero przygodę z tym) a nie wiem jak to rozwiązać ?