funkcja logarytmiczna
Misiek: Do wykresu funkcji logarytmicznej należy punkt A(2 ;−1). Rozwiąż równanie |f(x−1)|=3.
Pierwszą część zadania obliczyłem i wyszło mi a=1/2. Podpowie mi ktoś w jaki sposób rozwiązać
tą nierówność?
Mam podstawić po prostu log12x za |f(x−1)|?
25 paź 16:09
Bizon:
... zacznij od napisania pełnej treści zadania
25 paź 17:44
Janek191:
log
a x = f(x)
A = ( 2; − 1) należy do wykresu funkcji f , więc
log
a 2 = − 1 ⇔ a =
12
czyli
f(x) = log
12 x
I f( x− 1) I = 3
I log
12 ( x − 1) I = 3 ⇔ log
0,5 ( x − 1) = − 3 lub log
0,5 ( x − 1) = 3 ⇔
| | 1 | |
⇔ x − 1 = (U{1}[2})−3 lub x − 1 = ( |
| )3 ⇔ |
| | 2 | |
| | 1 | |
⇔ x − 1 = 23 lub x − 1 = |
| ⇔ |
| | 8 | |
| | 1 | | 1 | |
⇔ x = 8 + 1 = 9 lub x = 1 + |
| = 1 |
| |
| | 8 | | 8 | |
Dziedzina : x − 1 > 0 ⇒ x > 1
=========================
25 paź 18:02
Mila:
f(x)=log
12(x) i x>0
f(x−1)=log
12(x−1)
|log
12(x−1)|=3 i x−1>0⇔x>1⇔
log
12(x−1)=3 lub log
12(x−1)=−3
teraz dokończysz?
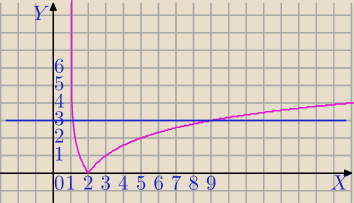
Graficznie zobacz. Są dwa rozwiązania.
g(x)=|log
12(x−1)|
h(x)=3
25 paź 18:12
 f(x)=log12(x) i x>0
f(x−1)=log12(x−1)
|log12(x−1)|=3 i x−1>0⇔x>1⇔
log12(x−1)=3 lub log12(x−1)=−3
teraz dokończysz?
Graficznie zobacz. Są dwa rozwiązania.
g(x)=|log12(x−1)|
h(x)=3
f(x)=log12(x) i x>0
f(x−1)=log12(x−1)
|log12(x−1)|=3 i x−1>0⇔x>1⇔
log12(x−1)=3 lub log12(x−1)=−3
teraz dokończysz?
Graficznie zobacz. Są dwa rozwiązania.
g(x)=|log12(x−1)|
h(x)=3