Rozwiąż równanie Kasia: ³√x²+x=2 = √x²+x+2

ICSP: i w czym problem ?

Kasia: problem jest od początku, założenia ok, ale co więcej to nie wiem

ICSP: Skoro dwie strony są dodatnie ( na podstawie założeń) to możesz podnieść to równanie do potęgi 6.

Kaja: podnieś obustronnie do potęgi 6.

ICSP: Innym pomysłem może być zastosowanie podstawienia t⁶ = x² + x + 2

Kasia: i rozwiązać (x²+x+2)²=(x²+x+2)³ ?

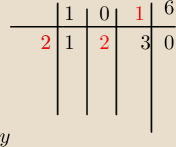
Enigma: Kasiu Jeśli w pierwszym pierwiastku jest −2 to zrobiłam: podnosimy obustronnie / do potęgi 3 x²+x−2=x³+x²+4 x³−x+6=0 (teraz tabelka Hornera) czerwone liczby są ujemne powstało (x+2) zawsze się zmienia znak, i (x²−2x+3) jeśli nie umiesz tej tabeli to napisz, może wyjaśnie.

Kasia: umiem umiem, a w pierwszym równaniu jest +2 zamiast =2

Enigma: no to w takim razie podstawiasz sobie +2 zamiast − i robisz analogicznie.. wyszytko jasne?

Kasia: tylko że (√x²+x+2)³ to nie jest x³+x²+4 jak napisałaś

ICSP: (x² + x + 2)³ − (x² + x + 2)² = 0 (x² + x + 2)² [x² + x + 2 − 1] = 0 x² + x + 2 = 0 v x² + x + 1 = 0 Obydwa równania są sprzeczne zatem i nasze początkowe równanie również jest sprzeczne.

Kasia: dobra, ostatnie pytanie jak przejść z (x² + x + 2)³ − (x² + x + 2)² = 0 do (x² + x + 2)² [x² + x + 2 − 1] = 0 ?

ICSP: a gdyby zamiast (x² + x + 2) było t. To czy potrafisz rozwiązać takie równanie : t³ − t² = 0 ?

Kasia: no potrafię, super dzięki