Trójkąt bez wartości kątów Anka: Dany jest trójkąt ABC, w którym AB=8, AC=6. Dwusieczna kąta CAB przecina bok BC w punkcie D takim, że AD=BD. Wyznacz długość boku BC. Ktoś wie jak to zrobić? Próbowałam użyć twierdzeń sinusów i cosinusów, ale bez jakichkolwiek miar kątów mam prawie same niewiadome, a rysunek (http://pl.tinypic.com/view.php?pic=2r2rfnt&s=5#.UmkOyafLQpI) nie może mi jakoś pomóc.

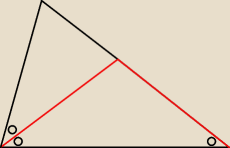
Janek191: Niech I ∡ CAB I = 2 α AB = 8 AC = 6 AD = BD Niech x = BC Z tw. cosinusów mamy x² = 6² + 8² − 2*6*8* cos 2α = 36 + 64 − 96 cos 2α = 100 − 96 cos 2α więc BC = x = √ 100 − 96 cos 2α ======================== Z tw. sinusów mamy

6		8		8
	=		=
sin α		sin ( 180o − 3α)		sin 3α

6 sin 3α = 8 sin α / : 2 3 sin 3α = 4 sin α 3*( 3 sin α − 4 sin³ α ) = 4 sin α 9 sin α − 12 sin³ α = 4 sin α 12 sin³ α = 5 sin α / : sin α 12 sin² α = 5

	5
sin2 α =
	12

	12		5		7
cos2 α = 1 − sin2 α =		−		=
	12		12		12

zatem

	7		5		2
cos 2α = cos2 α − sin2 α =		−		=		= U{1}{6]
	12		12		12

czyli BC = √ 100 − 96*u{1}[6} = √ 100 − 16 = √84 = √4*21 = 2 √21 Odp. BC = 2 √21 ≈ 9,16 ===============

asdfghjk: ΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ ΩΩΩΩΩΩΔΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩΩ

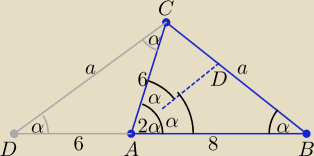
Bogdan: Z warunków zadania wynika, że trójkąt DBC jest równoramienny. Z podobieństwa trójkątów

	a		6
DBC i DAC otrzymujemy:		=		⇒ a2 = 84 ⇒ a = 2√21
	14		a