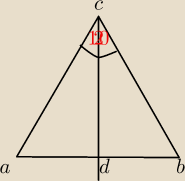
planimetria sosadbutidontknow: W trójkącie ABC mamy podane dwa boki : a oraz 2a i ∡C=120 stopni oraz dwusieczną, która dzieli bok AB w punkcie D. Oblicz DB

Aga1.: Które boki mają długość a i 2a? Przez a oznaczono wierzchołek.

sosadbutidontknow: ale wierzchołki to duże litery, tylko tutaj się nie da tak wpisać. Bok AC=2a, bok CB=a

sosadbutidontknow: żebym tylko wiedziała jak dojśc do tego, że bok AB=a√7 to dalej zrobię

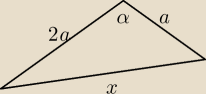
Aga1.: α=120⁰ Z twierdzenia cosinusów

	1
x2=a2+4a2−2*a*2a*cos1200, a cos1200=cos(1800−600)=−cos600=−
	2

x²=5a²+2a²=7a² x=√7a²=a√7.

Antek: masz kat , masz dwa boki wiec z twierdzenie cosinusow i oblicz AB

sosadbutidontknow: dziękuję Aga1