Funkcja
bezendu:
Dana jest funkcja f(x)=min(3, x2−5x+7), gdzie (a,b) oznacza nie większą z liczb a,b.
Wyznacz zbiór wartości ?
23 paź 22:45
Trivial:
23 paź 22:50
bezendu:
Jak to rozwiązałeś ?
23 paź 22:56
Trivial:
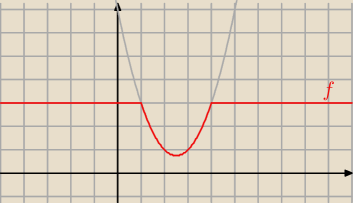
To tutaj trzeba coś rozwiązywać? Dla każdego x decydujesz co ma mniejszą wartość
3 czy może x2−5x+7. Wartość ta jest wartością funkcji f. Narysowałem sobie wykres funkcji
x2−5x+7 oraz 3 na szaro. Następnie wybrałem odpowiednie części.
23 paź 22:58
bezendu:
Dzięki teraz już rozumiem

23 paź 22:59
Piotr 10: Minimum dwóch liczb rzeczywistych a oraz b definiujemy następująco:
a dla a≤b
min(a;b)= b dla a>b
| | 1 | | 1 | | 1 | |
A więc, np. min(−3,1)=−3 min( |
| ; |
| )= |
| |
| | 2 | | 2 | | 2 | |
23 paź 22:59

