Stereometria
DeDee: Objętość sześcianu wynosi 343cm
3. Na jego krawędziach wychodzących z jednego wierzchołka
zaznaczono punkty odległe o 3 cm od tego wierzchołka i odcięto naroże o takich krawędziach.
Oblicz objętość odciętej części
W odpowiedziach jest 4,5

Za nic nwm nawet jak to wygląda
23 paź 21:03
krystek:
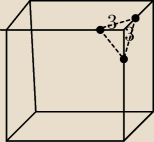
23 paź 21:07
DeDee: hm... no to podstawa łatwo h= (9√3)/2 a jak policzyć wysokość tych trójkącików?
23 paź 21:16
dero2005:
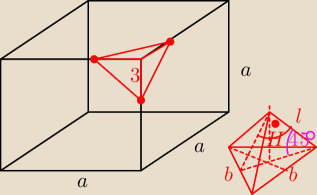
V = a
3 = 343
a =
3√343 = 7
b = 3
√2
policz objetość tego czerwonego stwora i wyjdzie 4,5
23 paź 21:24
Janek191:
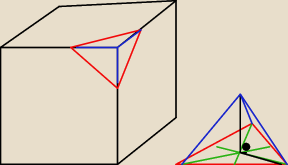
V = a
3 = 343 cm
3 ⇒ a =
3√343 cm3 = 7 cm
b
2 = 3
2 + 3
2 = 9 + 9 = 9*2 ⇒ b =
√9*2 = 3
√2
b = 3
√2 cm − długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego − długość
czerwonego odcinka
| | √3 | | √3 | | √3 | |
Pp = b2 |
| = ( 3 √2)2 |
| = 18* |
| = 4,5√3 − pole podstawy |
| | 4 | | 4 | | 4 | |
tego ostrosłupa
P
p = 4,5
√3 cm
2
3 cm − długość krawędzi bocznych odciętego ostrosłupa ( niebieskiego odcinka )
h
p − wysokość trójkąta równobocznego
| | √3 | | √3 | | 3√6 | |
hp = b |
| = 3p{2]* |
| = |
| |
| | 2 | | 2 | | 2 | |
| | 2 | | 3√6 | |
x = U{2}{3] hp = |
| * |
| = √6 |
| | 3 | | 2 | |
h − wysokość ostrosłupa
Z tw. Pitagorasa mamy
h
2 + x
2 = 3
2
h
2 = 9 − (
√6)
2 = 9 − 6 = 3 więc h =
√3
Objętość odciętego ostrosłupa
| | 1 | | 1 | | 1 | |
V = |
| Pp*h = |
| *4,5 √3 cm2 *√3 cm = |
| *4,5* 3 cm3 = 4,5 cm3 |
| | 3 | | 3 | | 3 | |
===================================================================
23 paź 21:35
Atonaj95:
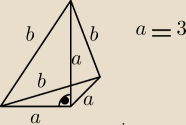
Najszybciej chyba jest potraktować wycinek w ten sposób
23 paź 21:49
Janek191:
@Atonaj95
Faktycznie − najlepszy sposób

| | 1 | | 1 | |
V = |
| PP *h = |
| *0,5 *32 * 3 = 0,5*9 = 4,5 |
| | 3 | | 3 | |
23 paź 22:02
 Za nic nwm nawet jak to wygląda
Za nic nwm nawet jak to wygląda

 V = a3 = 343
a = 3√343 = 7
b = 3√2
policz objetość tego czerwonego stwora i wyjdzie 4,5
V = a3 = 343
a = 3√343 = 7
b = 3√2
policz objetość tego czerwonego stwora i wyjdzie 4,5
 V = a3 = 343 cm3 ⇒ a = 3√343 cm3 = 7 cm
b2 = 32 + 32 = 9 + 9 = 9*2 ⇒ b = √9*2 = 3√2
b = 3√2 cm − długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego − długość
czerwonego odcinka
V = a3 = 343 cm3 ⇒ a = 3√343 cm3 = 7 cm
b2 = 32 + 32 = 9 + 9 = 9*2 ⇒ b = √9*2 = 3√2
b = 3√2 cm − długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego − długość
czerwonego odcinka
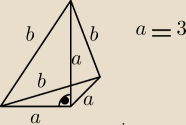 Najszybciej chyba jest potraktować wycinek w ten sposób
Najszybciej chyba jest potraktować wycinek w ten sposób
