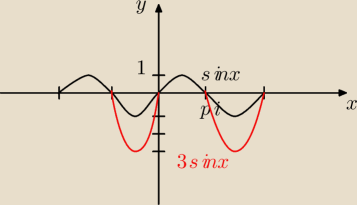
Naszkicuj wykres funkcji wajdzik: Naszkicuj wykres funkcji określonej wzorem f(x)=2sinx−|sinx| dla x∊<−2π,2π>. {sinx , dla sinx≥0 {3sinx , dla sinx<0

wajdzik:

	|f(x)|
To się powinno jako tako zgadzać ale mam problem, jak narysować funkcję g(x)=
	f(x)

dla x∊<−2π,2π>

Hajtowy: A uczyli jak rysować f(|x|) , |f(x)|, f(x) ?

wajdzik: uczyli ale nie za bardzo pamiętam, dobra, to ja coś wykombinuję a Ty to sprawdź

wajdzik: raczej bardziej mam problemem z tym:

	2|3sinx|
g(x)=		,
	3sinx

mam to teraz rozdzielić na dwa przypadki..?

wajdzik:

Lorak: tak, będą dwa przypadki.

wajdzik: g(x)= 2sinx, gdy sinx≥0 −2sinx, gdy sinx<0 zgadza się?

MQ:

	|f(x)|
g(x)=		=sgn(f(x)) poza punktami gdzie f(x)=0
	f(x)

dla wyjaśnienia: sgn(x)=1 dla x>0 = −1 dla x<0 w zasadzie 1 powinno być dla ≥0, ale w naszym przypadku, ze względu na dzielenie, jesteśmy poza dziedziną.

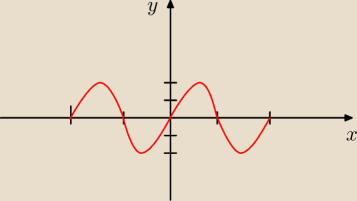
wajdzik: mam nadzieję, że jest ok

Lorak: post 19:40, źle wajdzik 3sinx się skrócą przecież

Mila:

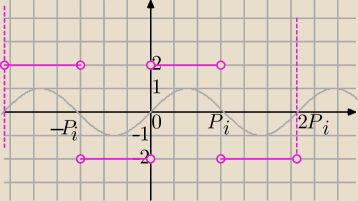
	2*|sinx|
g(x)=		i sinx≠0
	sinx

1) |sinx|=sinx dla sinx>0 ⇔x∊(0,π)U(−2π,π) wtedy:

	2sinx
g(x)=		=2
	sinx

2) |sinx|=−sinx dla sinx<0⇔dla x∊(π,2π)U(−π,0) Wtedy:

	2*(−sinx)
g(x)=		=−2
	sinx

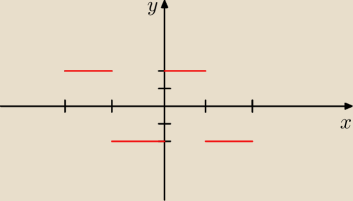
wajdzik: czyli będzie bez sinusów? jak to ? czyli wyjdzie coś takiego:

wajdzik: rozumiem! dzięki wielkie

Mila: To pięknie. Zapomniałeś o kółeczkach pustych na końcach gałązek.