Zbadaj monotonicznosc i ekstrema funkcji
iv : :
5 paź 20:06
iv : Ktos pomoze ? Jak to zrobic ?
5 paź 20:26
Bogdan:
Określ założenia, potem wyznacz pierwszą pochodną funkcji, badając znak pochodnej
określisz monotoniczność funkcji i wyznaczysz jej ekstremum.
5 paź 20:32
iv : dziedzina : x nalezy do rzeczywistych / {2, −2} tak ? a pochodna pierwsza to :
| | 3x2 (4−x2) − 2x* x3 | |
f'(x)= |
| dobrze robie ? ale co dalej ? |
| | (4−x2)2 | |
5 paź 20:39
iv : dalej bedzie :
| | 3x2(x−2)(x+2) | |
f'(x) = U {12x2 − x4}{(4−x)4} = |
| |
| | (4−x)4 | |
f(x) = 0 <=> x=2 x= −2 nast robie f(2) i f(−2) ?
5 paź 20:52
ivee: Moze ktos to sprawdzic czy robie to dobrze ?
7 paź 10:54
AS: Pochodna źle obliczona
| | 3x2*(4 − x2) − x3*(−2x) | | 12*x2 − 3*x4 + 2*x4 | |
f'(x) = |
| = |
| = |
| | (4 − x2)2 | | (4 − x2)2 | |
| 12*x2 − x4 | | x2*(12 − x2) | |
| = |
| = |
| (4 − x2)2 | | (4 − x2)2 | |
| x2*(2*√3 − x)*(2*√3 + x) | |
| |
| (4 − x2)2 | |
7 paź 11:47
Bogdan:

Dzień dobry.
Jeszcze raz (podaję pełne rozwiązanie):
Założenia: 4 − x
2 ≠ 0 ⇒ x
2 − 4 ≠ 0 ⇒ (x − 2)(x + 2) ≠ 0 ⇒ x ≠ −2 i x ≠ 2
D: x ∊ R \ {−2, 2}.
| | 3x2(4 − x2) + 2x*x3 | | 12x2 − 3x4 + 2x4 | |
f'(x) = |
| = |
| = |
| | (4 − x2)2 | | (x2 − 4)2 | |
| | −x2 (x2 − 12) | | −x2(x − 2√3)(x + 2√3) | |
= |
| = |
| |
| | (x − 2)2(x + 2)2 | | (x − 2)2(x + 2)2 | |
Zapisujemy wyrażenie wymierne w postaci wielomianowej i szkicujemy "falę":
W(x) = −x
2 (x − 2
√3) (x + 2
√3) (x − 2)
2) (x + 2)
2
pierwiastki: x = 0, x = 2
√3, x = −2
√3, x = 2, x = −2
Monotoniczność:
Funkcja f(x) jest rosnąca dla x ∊ (−2
√3), (−2, 0), (0, 2), (2, 2
√3);
Funkcja f(x) jest malejąca dla x ∊ (−
∞, −2
√3), (2
√3, +
∞).
Ekstrema:
Funkcja posiada minimum dla x = −2
√3 równe y
min = f(−2
√3) = 3
√3.
Funkcja posiada maksimum dla x = 2
√3 równe y
max = f(2
√3) = −3
√3
I to wszystko

7 paź 12:25
ola: f(x) = x2 + 2x + 2 (przez)
x+1
mam problem z policzeniem pochodnej. musze zbadac monotonicznosc i eksterma. pilnie. prosze o
pomoc
14 wrz 13:00
rumpek: | | x2 + 2x + 2 | | (x2 + 2x + 2)'*(x + 1)−(x2 + 2x + 2)(x + 1)' | |
f'(x)=( |
| )' = |
| |
| | x + 1 | | (x + 1)2 | |
| | (2x + 2)*(x + 1)−(x2+2x+2)*1 | | 2x2 + 2x + 2x + 2 − x2 − 2x − 2 | |
= |
| = |
| |
| | (x + 1)2 | | (x + 1)2 | |
14 wrz 13:06
kujon: βδπΔ≤⊂⇒∑
26 sty 19:30
manu: Zbadaj monotonicznosc i ekstrema funkcji
czy moze mi ktos pomoc zrobic ten przklad? bardzo prosze
30 sty 09:31
Aga1.: Zacznij od dziedziny
Oblicz pochodną tej funkcji ,oblicz miejsca zerowe pochodnej i zbadaj znak pochodnej.
30 sty 09:50
Gosia: f(x) = 2x4 + 4x2 + 1
31 sie 16:03
Aga1.:
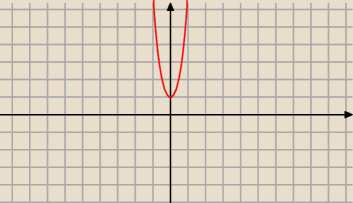
31 sie 19:49
Lol: Zbadaj monotoniczność funkcji na podstawie definicji f(x)=x3 dla x należącego do R
7 lis 14:25
magda: f(x)=x+√1−x
27 lis 19:32
Asia: Hej

mógłby ktoś mi pomóc
Polecenie : Zbadaj czy dana funkcja jest różniczkowalna
0 x=1
To w klamerce powinno być ale nie wiem jak ją zrobić

10 sty 16:35
anka: 4x3−9x2−8x−12 jak obliczyć
8 cze 22:14
 Dzień dobry.
Jeszcze raz (podaję pełne rozwiązanie):
Dzień dobry.
Jeszcze raz (podaję pełne rozwiązanie):


 mógłby ktoś mi pomóc
Polecenie : Zbadaj czy dana funkcja jest różniczkowalna
mógłby ktoś mi pomóc
Polecenie : Zbadaj czy dana funkcja jest różniczkowalna
