pomocy aaania: f. kwadratowa f ma tylko jedno miejsce zerowe, a osią symertii jej wykresu jest prosta o

	4
równaniu x−5=0. Do wykresu funkcji f należy punkt A(2, −1		). Napisz wzór funkcji w
	5

postaci ogólnej.

Janek191: Δ = 0 ⇒ q = 0 x − 5 = 0 ⇒ x = 5 ⇒ p = 5

	4		9
A = ( 2; − 1		) ⇒ f(2) = −
	5		5

f(x) = a*( x − p)² czyli

	9
f(x) = a*( x − 5)2 ⇒ f(2) = a*( 2 − 5)2 = −
	5

	9
a*( − 3)2 = −
	5

	9
9a = −
	5

	1
a = −
	5

zatem

	1
f(x) = −		( x − 5)2 = − 0,2 *( x2 − 10 x + 25) = − 0,2 x2 + 2x − 5
	5

Odp. f(x) = − 0,2 x² + 2x − 5 ======================

Janek191: Δ = 0 ⇒ q = 0 x − 5 = 0 ⇒ x = 5 ⇒ p = 5

	4		9
A = ( 2; − 1		) ⇒ f(2) = −
	5		5

f(x) = a*( x − p)² czyli

	9
f(x) = a*( x − 5)2 ⇒ f(2) = a*( 2 − 5)2 = −
	5

	9
a*( − 3)2 = −
	5

	9
9a = −
	5

	1
a = −
	5

zatem

	1
f(x) = −		( x − 5)2 = − 0,2 *( x2 − 10 x + 25) = − 0,2 x2 + 2x − 5
	5

Odp. f(x) = − 0,2 x² + 2x − 5 ======================

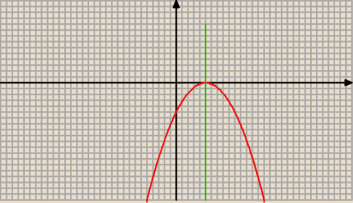Janek191: Wykres funkcji f(x) = − 0,2 x² + 2x − 5