krzywe
zadanie: (x−3)2+4y2=9 bedzie to rownanie elipsy
ale jak je przeksztalcic?
22 paź 14:47
zadanie: (x−3)
2+4
y2=9 /:9
jest to rownanie elipsy
dobrze?
22 paź 14:57
Mila:
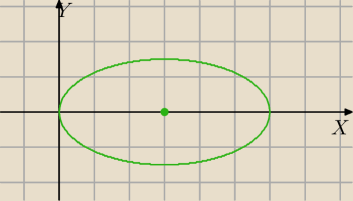
Zgadza się.
S=(3,0)
a=3
22 paź 15:24
zadanie: dziekuje
22 paź 15:26
zadanie: jeszcze taki przyklad:
2x
2+3y+2y
2=0
| | 3 | | 9 | | 9 | |
2x2+2(y2+ |
| y+ |
| )− |
| =0 |
| | 2 | | 16 | | 8 | |
| | 3 | | 9 | |
x2+(y+ |
| )2= |
| → jest to okrag |
| | 4 | | 16 | |
dobrze?
22 paź 15:33
Mila: Za chwilę. Pisz następne przykłady.
22 paź 15:37
krystek: Tak
22 paź 15:39
Mila:
Trzeba było najpierw podzielić przez 2.
Wtedy prościej.
22 paź 15:46
zadanie: dziekuje
22 paź 15:51
zadanie: 2x−3y
2+6y=0
2x−3(y
2−2y+1)+3=0
2x−3(y−1)
2+3=0
2x+3=3(y−1)
2 /:2
| | 3 | | 3 | | 3 | |
x+ |
| = |
| (y−1)2 (ogolnie: x= |
| y2 tylko przesunieta) |
| | 2 | | 2 | | 2 | |
| | 3 | |
jest to parabola o wierzcholku w punkcie (− |
| , 1) |
| | 2 | |
22 paź 15:55
zadanie: ostatni przyklad narazie
xy−x−1=0
xy=x+1/:x wtedy x≠0 bo nie moge dzielic przez 0
jest to hiperbola
dobrze?
mozna inaczej? np. wylaczajac x przed nawias i dzielac przez (y−1) ale wtedy y≠1
to chyba nie byloby to samo prawda?
22 paź 16:04
Mila:
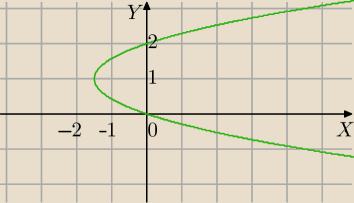
Dobrze.
22 paź 16:11
Mila:
xy−x−1=0 dla x=0 nie jest spełnione równanie.
hiperbola.
dobrze.
22 paź 16:14
zadanie: dziekuje
22 paź 16:20
zadanie:
{(x−2)
2+(y−1)
2=4
jak rozwiazac taki uklad rownan? mozna to odjac stronami?
22 paź 17:31
Mila: Mozna .
22 paź 18:02
Mila:

Zbadaj odległość środków.
Brak rozwiązań.
22 paź 18:11
zadanie: dziekuje
a gdyby byla taka sytuacja, ze dwa okregi nachodza na siebie
to ile wtedy mialyby punktow wspolnych?
nieskonczenie wiele czy skoczenie wiele?
22 paź 18:30
zadanie: dane sa punkty A(−1,1) i B(3,−1). Znajdz zbiory punktow X, dla ktorych srodek odcinka AX lezy
na okregu o srodku w punkcie (3,3) i promieniu 1.
X=(x, y)
| | x−1 | | y+1 | |
srodek odcinka AX to punkt o wspolrzednych ( |
| , |
| ) |
| | 2 | | 2 | |
rownanie tego okregu to: (x−3)
2+(y−3)
2=1
czyli teraz do rownania okregu musze podstawic wspolrzedne srodka odcinka za x podstawiam
| x−1 | | y+1 | |
| a za y podstawiam |
| tak? |
| 2 | | 2 | |
wtedy wychodzi mi okrag o rownaniu (x−7)
2+(y−5)
2=4
i teraz okrag (x−7)
2+(y−5)
2=4 oraz okrag (x−3)
2+(y−3)
2=1 musza miec jakies punkty wspolne
czyli musze rozwiazac uklad rownan? dobrze?
22 paź 19:07
zadanie: ?
22 paź 19:32
Mila:
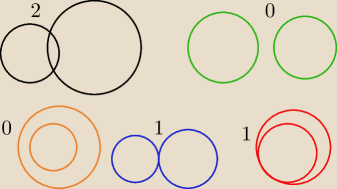
Dwa okręgi o jednakowych promieniach mogą mieć dwa punkty wspólne( przecinają się),
jeden(styczne zewnętrznie) , o ( nie mają ), nieskończenie wiele ( współśrodkowe).
O różnych promieniach podaję na rysunku.
22 paź 19:36
Mila:
Następne zadanie później.
22 paź 19:37
zadanie: dziekuje
22 paź 20:00
zadanie: 1. jakie figury przedstawiaja nastepujace rownania?
a) x2+y2<4 ; jest to kolo bez brzegu
b) (x−8)2+(y+1)2=0 ; jest to punkt o wspolrzednych (8, −1)
tak?
2. Dany jest punkt A nie lezacy na osi Ox. Uzasadnij, ze zbior punktow X, dla ktorych odleglosc
od A jest taka sama jak odleglosc od osi Ox jest parabola. Jaki punkt jest wierzcholkiem tej
paraboli?
A(xa, ya)
X(x.y)
B(x,0)
IAXI=IBXI ale wtedy mam za duzo niewiadomych. moze inaczej to oznaczyc?
22 paź 22:19
zadanie: B(xb,0)
22 paź 22:19
zadanie: Znajdz rownania prostych zawierajcych wysokosci w trojkacie o wierzcholkach A(2,1), B(−1,3)
C(−2,−1). sprawdz, ze przecinaja sie one w jednym punkcie.
BX o AC=0 (lub CA)
CX o AB=0 (lub BA)
AX o CB =0 (lub BC)
gdzie X(x,y)
dobrze?
tylko teoretycznie ten punkt za kazdym razem jest inny
22 paź 23:29
zadanie: mozna tez znalezc prosta AB i potem prosta przechodzaca przez punkt C i prostopadla do prostej
AB i analogicznie do pozostalych ale szukam szybszego sposobu
22 paź 23:32
Mila:
A=(a,b)
X=(x,y)
B=(x,0)
√(x−a)2+(y−b)2=|y| /
2
x
2−2ax+a
2+y
2−2by+b
2=y
2
x
2−2ax+a
2+b
2=2by
| | x2 | | a | | a2+b2 | |
y= |
| − |
| *x+ |
| parabola |
| | 2b | | b | | 2b | |
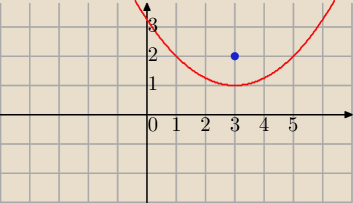
Dla A=(3,2) masz
(x
w,y
w)=(3,1)
23 paź 00:27
zadanie: dziekuje
23 paź 06:46
zadanie: jezeli to mozliwe to prosilbym rowniez o sprawdzenie pozostalych zadan
23 paź 06:47
zadanie: jezeli chodzi o to zadanie to nie wiedzialbym, ze takie rownanie przedstawia parabole
jest co prawda x2 potem x i wyraz wolny ale za duzo tych ulamkow
23 paź 06:51
Mila:
Dla ustalonego punktu A, jego współrzędne traktujesz jak stałe.
Zadanie z 19:07. Nie rozumiem po co tam dany jest punkt B
Czy całą treść zapisałeś?
23 paź 17:11
zadanie: tresc jest dobra tylko ten punkt B byl do innych podpunktow potrzebny a w tym wlasnie nie wiem
do konca jak to obliczyc?
23 paź 17:24
Mila:

S=(x
s,y
s)
Okrąg (x−7)
2+(x−5)
2=2
2 jest zbiorem szukanych punktów jako jednokładny do okręgu
(x−3)
2+(y−3)
2=1 w skali k=2 , względem punktu A
Z treści zadania wynika, że
AX
1=2AS
1
AX
1→=2AS
1→
Analogicznie :
AX
2→=2AS
2→
k=2 , Punkt A −środek jednokładności
23 paź 18:43
zadanie: dziekuje
23 paź 19:37
zadanie: czy dobrze jest zadanie 1 z godziny 22:19?
i jakas podpowiedz do zadania z 23:29?
23 paź 19:39
Mila:
Zadanie1) dobrze.
Następne zadanie ( nie zauważyłam go wcześniej), później. Teraz mam kolację.
Może napisz te równania, to porównam ze swoim rozwiązaniem.
23 paź 19:58
zadanie: | | 2 | | 7 | | 3 | |
AB: y=− |
| x+ |
| ; prosta C: y= |
| x+2 |
| | 3 | | 3 | | 2 | |
| | 1 | | 3 | |
BC: y=4x+7; prosta A: y=− |
| x+ |
| |
| | 4 | | 2 | |
| | 1 | |
AC: y= |
| x; prosta B: −2x+1 |
| | 2 | |
chcialem zrobic jakos z wektorami, zeby bylo szybciej ale zrobilem z prostymi dluzej ale jak
sie nie wie inaczej to lepiej dluzej niz sie zastanawiac bo nie ma czasu
23 paź 20:31
Mila:

A(2,1), B(−1,3), C(−2,−1). z przecinaja sie one w jednym punkcie.
AC
→=[−4,−2] i BX
→=[x+1,y−3]
AC
→◯ BX
→=[−4,−2]◯[x+1,y−3]=0 (wektory prostopadłe− iloczyn skalarny=0)⇔
−4x−4−2y+6=0 ⇔
y=−2x+1
AB
→=[−3,2] i CY
→=[x+2,y+1]
| | 3 | |
AB→◯CY→=[−3,2]◯[x+2,y+1]=−3x−6+2y+2=0⇔ y= |
| x+2 |
| | 2 | |
BC
→[−1,−4], i AZ
→[x−2,y−1]
BC
→ ◯AZ
→[−1,−4] ◯ [x−2,y−1]=0⇔−x+2−4y+4=0
Punkt przecięcia :
| | 3 | | −2 | | 4 | |
−2x+1= |
| x+2⇔x= |
| y=1 |
| |
| | 2 | | 7 | | 7 | |
dokończ.
23 paź 21:06
23 paź 21:15
zadanie: i juz ostatnie na dzisiaj zadanie
2013 i−1
∏ ∏ (pj{j}−pi{i})
i=2 j=1
jak rozpisac taka liczbe?
tam jest pierwiastek jotego stopnia z j minus pierwiastek itego stopnia z i
23 paź 21:36
zadanie: ?
24 paź 18:46
zadanie: moglbym prosic o rozpisanie?
24 paź 20:24
Mila:
i=2, to j=1 masz czynnik (1−√2)
i=3 to j=1do2 masz czynniki (1−3√3)*(√2−3√3)
i=4 to j=1 do 3 masz czynniki: (1−4√4)*(√2−4√4)*(3√3−4√4) ale zauważ, że 4√4=√2
czyli środkowy czynnik jest równy 0 i cały iloczyn jest równy 0
(1−√2)*(1−3√3)*(√2−3√3)*(1−4√4)*(√2−4√4)*(3√3−4√4) * ...=0
Jednak nie wiem, czy nie mam pomyłki, sprawdzaj z wykładem i tym co napisałam, może [Z[Godzio
]]tu spojrzy jest na bieżąco z tym materiałem.
24 paź 21:04
zadanie: dziekuje
24 paź 21:16
Mila:
Miałeś już kolokwium?
24 paź 21:17
zadanie: z analizy to juz 2 mialem
mam co tydzien
24 paź 21:39
cyco: Mila, ubek czy patriota

?
24 paź 21:43
zadanie: nie bylo pomylki
dziekuje
25 paź 19:59
zadanie: a jak obliczyc ile jest czynnikow w takim iloczynie? da sie?
25 paź 19:59
Mila:
Masz ciąg arytmetyczny
1+2+3+ .. n
n − oblicz ile czynników dla i=2013.
Zaliczyłeś kolokwia?
25 paź 20:42
Mila:
Do następnych zadań, załóż nowy wątek. Tu trzeba przewijac.
25 paź 20:44
zadanie: troche nie rozumiem
wyrazow w tym ciagu jest 2013 jezeli n=2013
u nas trzeba uzbierac odpowiednia liczbe punktow ze wszystkich kolokwiow
nie ma bezposredniego zalczenia jednego kolokwium
do tej pory mam w sumie 13 punktow na 20
26 paź 11:37
Mila:
Wg mnie n=2012
Gratulacje, 13 punktów/20 pkt , to nieźle jak na początek.
26 paź 16:44
zadanie: 
26 paź 18:39
 Zgadza się.
Zgadza się.
 Dobrze.
Dobrze.
 Zbadaj odległość środków.
Brak rozwiązań.
Zbadaj odległość środków.
Brak rozwiązań.
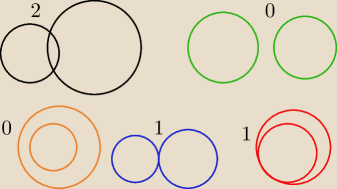 Dwa okręgi o jednakowych promieniach mogą mieć dwa punkty wspólne( przecinają się),
jeden(styczne zewnętrznie) , o ( nie mają ), nieskończenie wiele ( współśrodkowe).
O różnych promieniach podaję na rysunku.
Dwa okręgi o jednakowych promieniach mogą mieć dwa punkty wspólne( przecinają się),
jeden(styczne zewnętrznie) , o ( nie mają ), nieskończenie wiele ( współśrodkowe).
O różnych promieniach podaję na rysunku.
 A=(a,b)
X=(x,y)
B=(x,0)
√(x−a)2+(y−b)2=|y| /2
x2−2ax+a2+y2−2by+b2=y2
x2−2ax+a2+b2=2by
A=(a,b)
X=(x,y)
B=(x,0)
√(x−a)2+(y−b)2=|y| /2
x2−2ax+a2+y2−2by+b2=y2
x2−2ax+a2+b2=2by
 S=(xs,ys)
S=(xs,ys)
 A(2,1), B(−1,3), C(−2,−1). z przecinaja sie one w jednym punkcie.
AC→=[−4,−2] i BX→=[x+1,y−3]
AC→◯ BX→=[−4,−2]◯[x+1,y−3]=0 (wektory prostopadłe− iloczyn skalarny=0)⇔
−4x−4−2y+6=0 ⇔y=−2x+1
AB→=[−3,2] i CY→=[x+2,y+1]
A(2,1), B(−1,3), C(−2,−1). z przecinaja sie one w jednym punkcie.
AC→=[−4,−2] i BX→=[x+1,y−3]
AC→◯ BX→=[−4,−2]◯[x+1,y−3]=0 (wektory prostopadłe− iloczyn skalarny=0)⇔
−4x−4−2y+6=0 ⇔y=−2x+1
AB→=[−3,2] i CY→=[x+2,y+1]
 ?
?
