wartość bezwzględna
Lemon: Czy to jest prawda?
|a| < |b| ⇔ a<b ⋁ a<−b
Czy jakoś inaczej to powinno wyglądać?
że a<b to jestem pewny, ale nie wiem czy dalej alternatywa czy koniunkcja,
i czy zapisać a<−b czy jakoś inaczej.
21 paź 23:37
Lemon: up
22 paź 00:16
Mila:
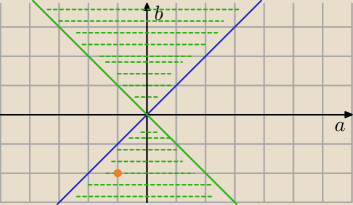
|a|<|b| /
2
a
2<b
2
a
2−b
2<0
(a−b)*(a+b)<0
a−b<0 i a+b>0 lub a−b>0 i a+b<0
a<b i a>−b lub a>b i a<−b
np.
(a,b)=(1,4)
|1|<|4|
(a,b)=(−1,−2)
|−1|<|−2| , −1>−2
22 paź 00:27
PW: Dla obu dodatnich nierówność |a| < |b| oznacza po prostu a<b,
dla obu ujemnych oznacza
−a < −b, czyli a>b,
a więc napisana przez Ciebie równoważność jest nieprawdziwa.
22 paź 00:32
PW: Zagapiłem się, Mila już odpowiedziała.
22 paź 00:37
Lemon: Dziękuję

22 paź 00:47
 |a|<|b| /2
a2<b2
a2−b2<0
(a−b)*(a+b)<0
a−b<0 i a+b>0 lub a−b>0 i a+b<0
a<b i a>−b lub a>b i a<−b
np.
(a,b)=(1,4)
|1|<|4|
(a,b)=(−1,−2)
|−1|<|−2| , −1>−2
|a|<|b| /2
a2<b2
a2−b2<0
(a−b)*(a+b)<0
a−b<0 i a+b>0 lub a−b>0 i a+b<0
a<b i a>−b lub a>b i a<−b
np.
(a,b)=(1,4)
|1|<|4|
(a,b)=(−1,−2)
|−1|<|−2| , −1>−2
