Rownania zespolone
seba: |z|i + Rez + Imz = 2i
21 paź 22:02
Trivial:
z = x + iy
z
1 =
√2(1 − i)
z
2 =
√2(−1 + i)
21 paź 22:07
ZKS:
Niech z = x + iy
|z|i + Re(z) + Im(z) = 2i
x + y = 0 ⇒ y = −x
√x2 + y2 = 2
√2|x| = 2
x = ±√2 ∧ y = ±√2
z = ±√2(1 + i).
21 paź 22:09
ZKS:
Jasne.
z = ±
√2(1
− i)
21 paź 22:10
seba: |z| to jest modul czyli sqrtRez2+Imz2
21 paź 22:14
seba: o to własnie choziło zks
21 paź 22:14
ZKS:
Rozwiązanie które pokazał Trivial jest duże lepsze.
21 paź 22:17
Trivial: Czemu lepsze?
21 paź 22:18
ZKS:
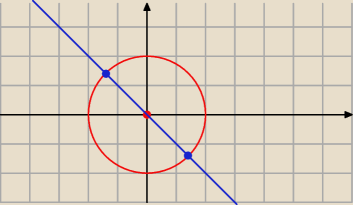
Żadnego praktycznie liczenia. Jako że jestem ślepy o tej porze po uczelni to nawet nie
zauważyłem że wystarczyło by zrobić tylko rysunek okręgu o środku w puncie (0 ; 0) i
promieniu 2 i prostej y = −x i od razu mamy rozwiązanie.
21 paź 22:22
Trivial: Jak kto woli.
21 paź 22:24
ZKS:
Wolę Twój.
21 paź 22:27