Ile ma rozwiązań Dawid: Równanie (X+2)²=16

bezendu: |x+2|=4 x+2=4 lub x+2=−4 x=2 lub x=−6

ZKS:

Piotr 10: (x+2)² − 4²=0 (x+2−4)(x+2+4)=0 x=2 v x= − 6

ZKS: To ja jeszcze policzę Δ oraz x₁ i x₂. Żartowałem.

Dawid: JA tak zrobiłem i jest git

bezendu: ZKS co ludzi straszysz

Piotr 10:

Piotr 10: (x+2)²=16 x²+4x+4=16 x²+4x−12=0 Δ=16+48=64 √Δ=8

	−4−8		−4+8
x1=		=−6 ⋁ x2=		=2
	2		2

bezendu: A jednak

Piotr 10: Delta rządzi

bezendu: x²+4x−12=0 x²−2x+6x−12=0 x(x−2)+6(x−2)=0 (x−2)(x+6)=0 x=2 lub x=−6

Piotr 10: Hahha Chyba wszystkie już sposoby zostały pokazane

bezendu: Do wyboru do koloru

Piotr 10: (x+2)²=16 *√ Ix+2I=4 Korzystam z interpretacji geometrycznej Szukam liczb na osi liczbowej, których odległość od liczby ''−2'' wynosi 4. Odp: x=−6 ⋁ x=2

bezendu: Rozważam w przedziałach: 1⁰ (−∞,−2) −x−2=4 −x=6 x=−6∊(−∞,−2) 2⁰ <−2,∞) x+2=4 x=2∊<−2,∞)

Piotr 10: No nie mogę

bezendu: Twój ruch..

matyk: Wszystkich sposobów nie jesteście w stanie pokazać

Piotr 10: Jeszcze graficznie można to zrobić. Narysować wykres y=IxI zrobić translację o wektor u^→=[−2;0] i odczytać dla jakich argumentów wartość funkcji wynosi 4

bezendu: Ja już pomysłu nie mam

Piotr 10: Wygrałem

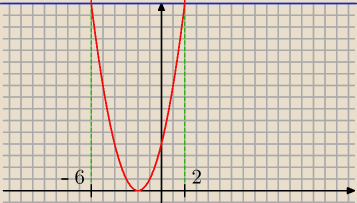
ZKS: Rysujemy parabolę y = (x + 2)² oraz prostą y = 16. Punkty przecięcia to nasze rozwiązanie. Z rysunku odczytujemy x = −6 oraz x = 2.

Piotr 10: I jak zawsze ZKS nas zniszczył

ZKS:

Piotr 10: Ulalala