Jak policzyć środek masy trójkąta równobocznego o boku a=1m, gdy mamy podane jego masy m1,m2
i m3 ?
Wiem jaki jest ogólny wzór środka masy itd. Robiłem zadania z tego już. Gdybym miał to w
układzie kartezjańskim to łatwo.
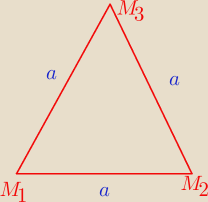Nie wiem czemu tak, ale kiedyś widziałem podobne zadanie. I mnie ciekawi jak to zrobić
| 2 | a√3 | |||
Może coś z promieniem okręgu opisane zdziałać? R= | * h h= | , ale i tak to mi nic | ||
| 3 | 2 |
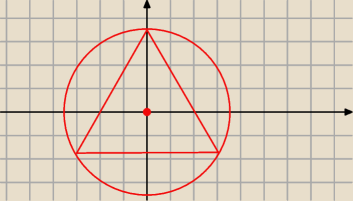Proszę, już jest w układzie kartezjańskim.
| x1*m1+x2*m2+x3*m3 | ||
x= | ||
| m1+m2+m+3 |
| 2 | ||
x3= | *h  m3 znajduje się na górze w wierzchołku | |
| 3 |
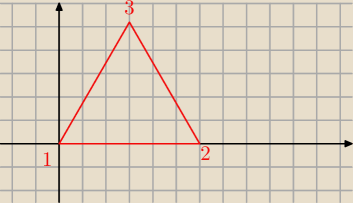Ogólny wzór wektorowy jest
| ∑i miri | ||
rśm = | ||
| M |
| m1*(0,0) + m2*(a,0) + m3*(12a,h) | ||
rśm = | ||
| m1+m2+m3 |
| m2 + 12m3 | ||
xśm = a* | ||
| M |
| √3m3 | ||
yśm = a* | ||
| 2M |