Zastosowanie funkcji kwadratowej
EC:

W trójkąt prostokątny równoramienny o przeciwprostokątnej długości 10 wpisujemy różne
prostokątyw sposób przedstawiony na rysunku. Jakie wymiary powinien mieć wpisany prostokąt,
aby jego pole było największe.
20 paź 18:46
Saizou :
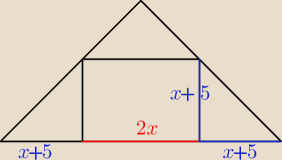
x∊(0:5)
zatem
P(x)=2x(x+5) i kiedy to jest największe
20 paź 18:53
EC:
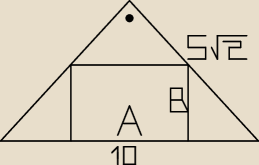
20 paź 18:53
EC: Dlaczego x ∊ (0,5) Jezeli przeciwprostokątna jest równa 10, to 2x rowne jest 0
20 paź 18:56
EC: ?
20 paź 19:00
EC:
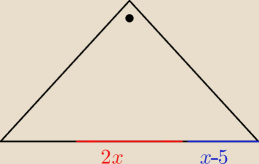
20 paź 19:10
Saizou : pomyliłem oznaczenia

zamiast 5+x miało być 5−x
20 paź 19:12
EC: ale co dalej, rozumiem tylko moj ostatni rysunek, dlaczego drugi bok prostokąta miałeś zamiar
oznaczyć przez x−5
20 paź 19:14
EC: ?
20 paź 19:21
Saizou :
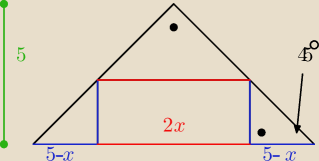
przeciwprostokątna ma dł 10 czyli 5−x+2x+5−x=10
| | 10−2x | |
ja oznaczyłem sobie 2x, bo |
| =5−x (żeby nie mieć ułamków) |
| | 2 | |
P(x)=2x(5−x) ←jest największe dla x
w (bo parabola ma ramiona skierowane do dołu )
x=0 x=5
P
max=2*(2,5)*(5−2,5)=5*2,5=12,5
20 paź 19:27
EC: Dzięki, wszystko jasne

20 paź 19:31
 W trójkąt prostokątny równoramienny o przeciwprostokątnej długości 10 wpisujemy różne
prostokątyw sposób przedstawiony na rysunku. Jakie wymiary powinien mieć wpisany prostokąt,
aby jego pole było największe.
W trójkąt prostokątny równoramienny o przeciwprostokątnej długości 10 wpisujemy różne
prostokątyw sposób przedstawiony na rysunku. Jakie wymiary powinien mieć wpisany prostokąt,
aby jego pole było największe.
 x∊(0:5)
zatem
P(x)=2x(x+5) i kiedy to jest największe
x∊(0:5)
zatem
P(x)=2x(x+5) i kiedy to jest największe


 zamiast 5+x miało być 5−x
zamiast 5+x miało być 5−x
 przeciwprostokątna ma dł 10 czyli 5−x+2x+5−x=10
przeciwprostokątna ma dł 10 czyli 5−x+2x+5−x=10
