Funkcja kwadratowa bezendu: Podaj wzór i naszkicuj wykres funkcji f przyporządkowującej każdej wartości parametru m, dla której istnieją dwa różne pierwiastki równania x²+2x+m=0, iloczyn pierwiastków tego równania.

Godzio: Dziedzin dla m: Δ > 0 Funkcja zmiennej m:

	m
f(m) = m (x1x2 =		= m )
	1

Godzio: Dziedzina*

bezendu: 4−4m>0 −4m>−4 4m<4 m<1 m∊(−∞,1) I co dalej ?

Godzio: No i rysujesz funkcję f(m) = m w przedziale (−∞.1)

bezendu: Wyznacz te wartości parametru m dla których równanie x²+mx+9 ma dwa rozwiązania mniejsze od −1 Δ>0 i co jeszcze w założeniach napisać ?

Godzio: Narysuj przykładowy wykres takiej funkcji, i zobacz co musi być spełnione, żeby to zachodziło

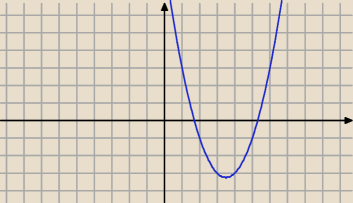
bezendu: dla m=−7

Godzio: No dobra, i teraz jak ta "−1" wpływa na wykres ?

bezendu: Dla m=−1 to równanie nie będzie miało pierwiastków ?

Godzio: Nie za bardzo o to mi chodziło, zaraz pokażę (sory, że tak późno odpisuje, ale sporo rzeczy mi się naschodziło )

Godzio: Niestety wykres mi nie chciał się wygenerować poprawnie, więc na razie masz same warunki: Δ ≥0 f(−1) > 0 x_w < −1

bezendu: Godzio nic nie szkodzi Czemu Δ≥0 a nie Δ>0 ?

Godzio: " dwa rozwiązania " Nic nie pisze, że mają być różne

bezendu: Godzio jak miałbyś jeszcze chwilkę to rzuć okiem

	⎧	y=6x+m
Dla jakich wartości parametru m układ równań	⎩	y=3x2−1	ma jedno rozwiązanie

6x+m=3x²−1 3x²−6x−m−1=0 Δ=0 36−12(−m−1)=0 36+12m+12=0 12m=−48 m=−4 ok ?

Piotr 10: Dla mnie we wcześniejszym zadaniu powinna być delta większa od zera. Bo jak mamy nawet pierwiastek dwukrotny to traktujemy go jako jeden a nie jako 2. A w poleceniu jest napisane, że ''dwa rozwiązania''. Ale wiem, że to różnie jest odbierane, była chyba nawet dyskusja o tym na forum jakiś czas temu

Piotr 10: