Fizyka - dynamika studia
Gustlik: Kochani, mam takie dwa dość skomplikowane zadania z fizyki, może ktoś potrafi je rozwiązać albo
udzielić wskazówek?
1. Ciało o masie m spada z wysokości H pod wpływem siły grawitacji mg i siły oporu
proporcjonalnej doprędkości kv. Wyznaczyć przyśpieszenie a(t), prędkość c(t), położenie x(t)
tego ciała. Warunki początkowe to v(0)=0 i z(0)=H. Wykazać, że dla małych czasów t<<m/k
| | k | gt2 | |
otrzymujemy przybliżenie v(t)≈−gt+ |
|
| i odpowiednio |
| | m | 2 | |
2. Wyznaczyć promień okręgu R i prędkość kątową ω w ten sposób, aby trajektoria okręgu
r
→(t)=[Rcos(ωt), Rsin(ωt), 0] była rozwiązaniem równania Newtona mr
→=−er
→xB
→ opisującego
ruch cząstki o masie m, ładunku −e, prędkości początkowej v
0→=[0, v, 0] w stałym polu
magnetycznym B
→=[0, 0, B]. Wyliczyć wektor siły Lorentza F
→(t).
Z góry dzięki za wskazówki lub rozwiązanie, bo dawno nie bawiłem się w takie zaawansowane
zadania fizyczne, a znajomy ma kolokwium z tego i potrzebuje pomocy. Całą resztę listy mu
zrobiłem, ale te na te dwa jak na razie nie mam pomysłu.
Krzysiek: 1.z tego co mi się wydaje wystarczy rozwiązać równanie różniczkowe:
mv'=kv−mg
| | gm | |
rozwiązując je otrzymujemy: v(t)=cek/mt+ |
| |
| | k | |
v(0)=0⇒c=−gm/k
różniczkując i całkując otrzymujemy również z(t) i a(t)
ale tych przybliżeń to nie wiem jak wykazać
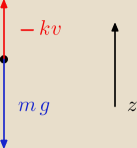 Z praw Newtona mamy:
ma = −kv − mg
Z praw Newtona mamy:
ma = −kv − mg