pomocy! iza: na plaszczyznie z prostokatnym ukladem wspolrzednych zilustruj zbior punktow ktorych wspolrzedne spelniaja nierownosc |y−1|≥ |x−2|+1

iza: niech ktoś pomoże...

ICSP: Jeśli nie masz innego pomysłu zawsze możesz rozpisać to na IV przypadki

iza: czyli jak? wytlumacz prosze

ICSP: 1. Szukasz miejsc zerowych wyrażeń pod wartością bezwzględną 2. Piszesz odpowiednie przedziały 1. y − 1 = 0 ⇒ y = 1 x − 2 = 0 ⇒ x = 2 I teraz 1^o Możemy mieć sytuacje że y−1 jest nieujemne oraz x − 2 jest nieujemne 2^o Możemy mieć sytuacje że y − 1 jest ujemne a x−2 nieujemne 3^o y − 1 ujemne , x−2 ujemne 4^o y − 1 nieujemne , x − 2 ujemne 1^o dla x ≥ 2 oraz y ≥ 1 mamy : y − 1 ≥ x − 2 + 1 ⇒ y ≥ x 2^o y < 1 oraz x ≥ 2 mamy : −y + 1 ≥ x − 2 + 1 ⇒ y ≤ −x + 2 Pozostałe dwa przypadki w identyczny sposób

iza: ok dziekuje, ale jak mam to przedstawic w ukladzie?

PW: Na przykład {(x,y): y=x} (zbiór par (x,y), w których y=x) umiesz narysować, to przecież prosta. A jeśli w tych parach ma być y≥x, to trzeba rysować także wyżej − tam gdzie igreki są większe. Kiedyś to był poziom gimnazjum.

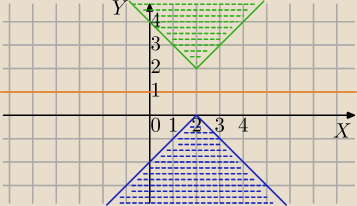
Mila: |y−1|≥ |x−2|+1 1) |y−1|=y−1 dla y≥1 część płaszczyzny nad prostą y=1 mamy nierówność: y−1≥ |x−2|+1⇔y≥ |x−2|+2 punkty nad prostą y=1 i nad wykresem y= |x−2|+2 2) |y−1|=−y+1 dla y<1 część płaszczyzny pod prostą y=1 mamy nierówność: −y+1≥ |x−2|+1⇔−y≥ |x−2|⇔ y≤−|x−2| punkty pod prostą y=1 i pod wykresem y= −|x−2|