Wyznacz równanie okręgu
Karol: Wyznacz równanie okrągu przechodzącego przez punkt (7, −1) i stycznego do prostej o równaniu:
x−y−4=0
19 paź 20:45
Janek191:
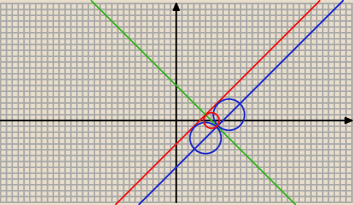
x − y − 4 = 0 ⇒ y = x − 4 − na rysunku kolor czerwony
P = ( 7; − 1)
Prosta równoległa do prostej o równaniu y = x − 4 przechodząca przez punkt P :
y = x + b
− 1 = 7 + b
b = − 8
y = x − 8 − na rysunku kolor niebieski
Odległość tych prostych
| | I C1 − C2 I | | I − 4 − (−8) I | | 4 | |
d = |
| = |
| = |
| = 2 √2 |
| | √ 12 + (−1)2 | | √2 | | √2 | |
Okrąg o środku P = ( 7; − 1) i promieniu r
1 = 2
√2
( x − 7)
2 + ( y + 1)
2 = ( 2
√2)
2
czyli ( x − 7)
2 + ( y + 1)
2 = 8
przecina prostą o równaniu y = x − 8 w dwóch punktach :
x
2 −14 x + 49 + ( x − 8 + 1)
2 = 8
x
2 − 14 x + 49 + x
2 − 14 x + 49 = 8
2 x
2 − 28x + 98 − 8 = 0
x
2 − 14x + 45 = 0
Δ = 196 − 4*1*45 = 196 − 180 = 16
√Δ = 4
| | 14 − 4 | | 14 + 4 | |
x1 = |
| = 5 x2 = |
| = 9 |
| | 2 | | 2 | |
y
1 = 5 − 8 = − 3 y
2 = 9 − 8 = 1
Mamy S
1 = ( 5; − 3) i S
2 = ( 9; 1 )
oraz równania okręgów stycznych do prostej o równaniu y = x − 4 przechodzących przez P:
( x − 5)
2 + ( y + 3)
2 = 8 i ( x − 9)
2 + ( y − 1)
2 = 8 na rysunku kolor
niebieski
============================================
Trzeci okrąg styczny ma środek leżący na prostej prostopadłej do prostej
o równaniu y = x − 4
y = − x + b
− 1 = − 7 + b
b = 6
y = − x + 6 na rysunku kolor zielony
−−−−−−−−−
r
3 =
√2
S
3 = ( a; b) b = − a + 6
| | 1*a + (−1)*b − 4 I | |
|
| = √2 |
| | √12 + (−1)2 | |
| I a − ( − a + 6) − 4 I | |
| = √2 |
| √2 | |
I 2a − 10 I = 2
2a − 10 = − 2 lub 2a − 10 = 2
2a = 8 lub 2a = 12
a = 4 lub a = 6
b = − 4 + 6 = 2 lub b = − 6 + 6 = 0
więc
S
3 = ( 6; 0 )
oraz równanie okręgu
( x − 6)
2 + y
2 = 2 na rysunku kolor czerwony
===============
19 paź 22:31
Janek191:
x − y − 4 = 0 ⇒ y = x − 4 − na rysunku kolor czerwony
P = ( 7; − 1)
Prosta równoległa do prostej o równaniu y = x − 4 przechodząca przez punkt P :
y = x + b
− 1 = 7 + b
b = − 8
y = x − 8 − na rysunku kolor niebieski
Odległość tych prostych
| | I C1 − C2 I | | I − 4 − (−8) I | | 4 | |
d = |
| = |
| = |
| = 2 √2 |
| | √ 12 + (−1)2 | | √2 | | √2 | |
Okrąg o środku P = ( 7; − 1) i promieniu r
1 = 2
√2
( x − 7)
2 + ( y + 1)
2 = ( 2
√2)
2
czyli ( x − 7)
2 + ( y + 1)
2 = 8
przecina prostą o równaniu y = x − 8 w dwóch punktach :
x
2 −14 x + 49 + ( x − 8 + 1)
2 = 8
x
2 − 14 x + 49 + x
2 − 14 x + 49 = 8
2 x
2 − 28x + 98 − 8 = 0
x
2 − 14x + 45 = 0
Δ = 196 − 4*1*45 = 196 − 180 = 16
√Δ = 4
| | 14 − 4 | | 14 + 4 | |
x1 = |
| = 5 x2 = |
| = 9 |
| | 2 | | 2 | |
y
1 = 5 − 8 = − 3 y
2 = 9 − 8 = 1
Mamy S
1 = ( 5; − 3) i S
2 = ( 9; 1 )
oraz równania okręgów stycznych do prostej o równaniu y = x − 4 przechodzących przez P:
( x − 5)
2 + ( y + 3)
2 = 8 i ( x − 9)
2 + ( y − 1)
2 = 8 na rysunku kolor
niebieski
============================================
Trzeci okrąg styczny ma środek leżący na prostej prostopadłej do prostej
o równaniu y = x − 4
y = − x + b
− 1 = − 7 + b
b = 6
y = − x + 6 na rysunku kolor zielony
−−−−−−−−−
r
3 =
√2
S
3 = ( a; b) b = − a + 6
| | 1*a + (−1)*b − 4 I | |
|
| = √2 |
| | √12 + (−1)2 | |
| I a − ( − a + 6) − 4 I | |
| = √2 |
| √2 | |
I 2a − 10 I = 2
2a − 10 = − 2 lub 2a − 10 = 2
2a = 8 lub 2a = 12
a = 4 lub a = 6
b = − 4 + 6 = 2 lub b = − 6 + 6 = 0
więc
S
3 = ( 6; 0 )
oraz równanie okręgu
( x − 6)
2 + y
2 = 2 na rysunku kolor czerwony
===============
19 paź 22:31