| 1 | ||
a) Naszkicuj wykres funkcji f określonej wzorem f(x) = | , gdzie x∊ R −{−3,3} | |
| |x|−3 |
| 1 | ||
b) Na podstawie wykresu funkcji f przeprowadź dyskusję liczby rozwiązań równania | =m | |
| |x|−3 |

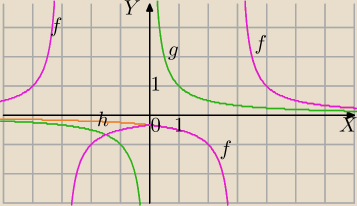 1)
Rysujesz wykres funkcji
1)
Rysujesz wykres funkcji
| 1 | ||
g(x)= | ||
| x |
| 1 | ||
2) przesuwasz o wektor [3,0]→h(x)= | ||
| x−3 |
| 1 | ||
pomijasz ⇒f(x)= | ||
| |x|−3 |
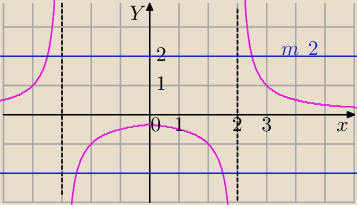
| 1 | ||
b) f(x)= | ||
| |x|−3 |
| 1 | |
=m | |
| |x|−3 |
| 1 | −1 | |||
f(0)= | = | |||
| 0−3 | 3 |
| −1 | ||
1) dla m< | równanie ma dwa rozwiązania (masz przykład dla m=−2) | |
| 3 |
| −1 | ||
2) dla m= | jedno rozwiązanie | |
| 3 |
| −1 | ||
3)dla m∊( | ,0> brak rozwiązań | |
| 3 |
 Próbuję to rozkminić
Próbuję to rozkminić
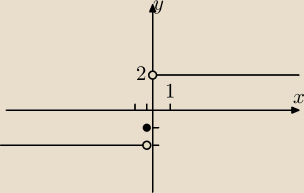 Coś takiego?
Coś takiego?
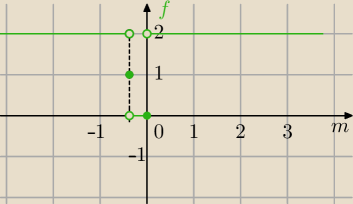
| −1 | ||
1) dla m< | dwa rozwiązania , f(m)=2 | |
| 3 |
| −1 | −1 | |||
2) dla m= | jedno rozwiązanie , f( | )=1 | ||
| 3 | 3 |
| −1 | ||
3) dla m∊( | ,0> brak rozwiązań, f(m)=0 | |
| 3 |
| −1 | ||
h( | )=1 | |
| 3 |

 Przedziały odczytujesz patrząc na wykres f(x) (19:15) i na niebieską linię, którą przesuwasz od
dołu do góry i określasz w ilu punktach przetnie się z wykresem f(x).
Zadanie 2)
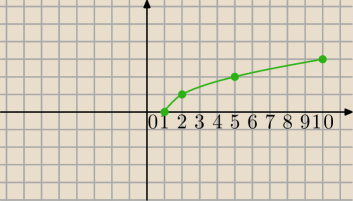
f(x)=√x−1 i x∊<1,10>
f(1)=√1−1=0
f(2)=√2−1=√1=1
f(5}=√5−1=√4=2
f(10)=√10−1=√9
Przedziały odczytujesz patrząc na wykres f(x) (19:15) i na niebieską linię, którą przesuwasz od
dołu do góry i określasz w ilu punktach przetnie się z wykresem f(x).
Zadanie 2)
f(x)=√x−1 i x∊<1,10>
f(1)=√1−1=0
f(2)=√2−1=√1=1
f(5}=√5−1=√4=2
f(10)=√10−1=√9
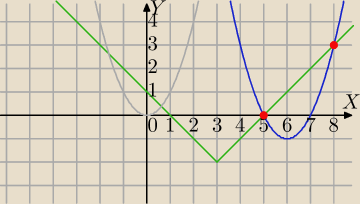 3)
Na podstawie wykresów odpowiednich funkcji wyznacz zbiór rozwiązań nie równości
√x2−6x+9−2 ≥(x−6)2 −1
f(x)=√x2−6x+9−2⇔f(x)=√(x−3)2−2⇔
f(x)=|x−3|−2
g(x)=(x2)→translacja T[6,−1]⇒h(x)=(x−6)2 −1
Masz odczytac dla jakich x−ów wykres funkcji f(x) (zielony) leży nad wykresem funkcji h(x) .
Czekam na Twoją odpowiedź.
3)
Na podstawie wykresów odpowiednich funkcji wyznacz zbiór rozwiązań nie równości
√x2−6x+9−2 ≥(x−6)2 −1
f(x)=√x2−6x+9−2⇔f(x)=√(x−3)2−2⇔
f(x)=|x−3|−2
g(x)=(x2)→translacja T[6,−1]⇒h(x)=(x−6)2 −1
Masz odczytac dla jakich x−ów wykres funkcji f(x) (zielony) leży nad wykresem funkcji h(x) .
Czekam na Twoją odpowiedź.
 zadanie 4
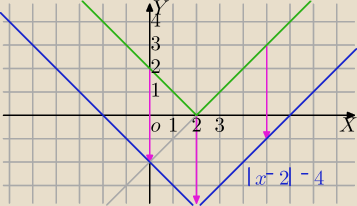
Naszkicuj wykres funkcji określonej wzorem f(x) = ||x−2|−4|. Na podstawie wykresu funkcji f
określ, dla jakich wartości parametru m (m∊R) równanie ||x−2|−4| = 7−5m ma trzy rozwiązania
dodatnie.
f(x)=||x−2|−4|
Wyjaśniam po kolei>
1) y=x−2 symetria względem OX tej części wykresu, która leży pod osią OX⇒
y=|x−2|→T[0,−4]⇒[N[y=|x−2|−4
Dokończę w następnym, abys lepiej widział zmiany.
zadanie 4
Naszkicuj wykres funkcji określonej wzorem f(x) = ||x−2|−4|. Na podstawie wykresu funkcji f
określ, dla jakich wartości parametru m (m∊R) równanie ||x−2|−4| = 7−5m ma trzy rozwiązania
dodatnie.
f(x)=||x−2|−4|
Wyjaśniam po kolei>
1) y=x−2 symetria względem OX tej części wykresu, która leży pod osią OX⇒
y=|x−2|→T[0,−4]⇒[N[y=|x−2|−4
Dokończę w następnym, abys lepiej widział zmiany.
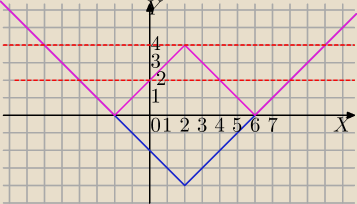 f(x)=||x−2|−4|
Wyjaśniam po kolei>
1) y=x−2 symetria względem OX tej części wykresu, która leży pod osią OX⇒
y=|x−2|→T[0,−4]⇒[N[y=|x−2|−4→
symetria względem OX tej części wykresu, która leży pod osią OX⇒
f(x)=||x−2|−4|
b) trzy rozwiązania dodatnie równania (punkty przecięcia między czerwonymi liniami )
||x−2|−4| =7−5m
dla
2<7−5m<4 rozwiąż.
f(x)=||x−2|−4|
Wyjaśniam po kolei>
1) y=x−2 symetria względem OX tej części wykresu, która leży pod osią OX⇒
y=|x−2|→T[0,−4]⇒[N[y=|x−2|−4→
symetria względem OX tej części wykresu, która leży pod osią OX⇒
f(x)=||x−2|−4|
b) trzy rozwiązania dodatnie równania (punkty przecięcia między czerwonymi liniami )
||x−2|−4| =7−5m
dla
2<7−5m<4 rozwiąż.
| 2 | 1 | |||
a Dziedzina funkcji g= −2 | ,3 | Dobrze? | ||
| 3 | 3 |
| 2 | 1 | |||
Dg= <−2 | , 3 | > * | ||
| 3 | 3 |