analiza PuRXUTM: no i kolejny problem

	x−1
Zbadaj bijektywność funkcji f(x)=		oraz wyznacz f−1 na f(dom(f))
	x+1

bijektywność=surjektywność + iniektywność iniektywność sprawdziłem, funkcja jest iniektywna no i teraz mam problem bo moim zdaniem nie jest surjektywna ponieważ:

	−2
f(x)=		+1 czyli nieprawda że ∀y∊Y ∃x∊X bo nie ma y=1
	x+1

a dalej w poleceniu jest wyznacz f⁻¹ a skoro nie jest bijekcją to się nie da. Zastanawia mnie jeszcze co oznacza wyznacz f⁻¹ na f(dom(f))

Janek191:

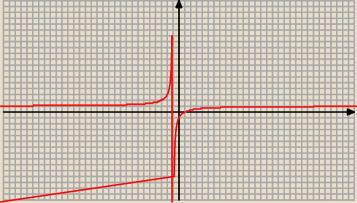
	x − 1
y =		; x ≠ − 1 − wykres czerwona hiperbola
	x + 1

więc x − 1 = y*( x + 1) x − 1 = y*x + y x − y*x = y + 1 ( 1 − y)*x = y + 1

	y + 1
x =
	1 − y

Po zamianie x na y i odwrotnie otrzymujemy funkcję odwrotną

	x + 1
y =		; x ≠ 1
	1 − x

− wykres niebieska hiperbola

PuRXUTM: Janek ale funkcja f jest bijektywna

Janek191:

	x − 1
y =		; x ≠ − 1
	x + 1

Przekształcenie ( funkcja ) jest więc trójką ( f, X, Y ); mówimy przy tym, że f jest funkcją o dziedzinie Dom f = X i przeciwdziedzinie Cod := f ( Dom f ) ⊆ Y. domaine − dziedzina codomaine − współdziedzina ( w Polsce używa się nazwy przeciwdziedzina )

Janek191: Na wykresie ten czerwony odcinek nie jest potrzebny − coś się dzieje z rysowaniem !

Janek191: Na wykresie ten czerwony odcinek nie jest potrzebny − coś się dzieje z rysowaniem !

Godzio: Co do funkcji, przy tak podanym poleceniu nie da się sprawdzić surjektywności

PuRXUTM: Godzio : no ale takie jest polecenie...czyli co mam zrobić ? Chyba wiem o co Ci chodzi. Że nie ma podanej dziedziny, tak ?

Godzio: Żeby rozwiązywać takie zadania musi być napisane "Sprawdź .... funkcji f : X → Y o wzorze f(x) = ... " Jak mamy padać czy wszystkie wartości są osiągnięte skoro nie wiemy jaka jest przeciwdziedzina

Godzio: Wkradła się literówka: "badać" I nie chodzi o dziedzinę, tylko o przeciwdziedzinę

PuRXUTM: czyli jak takie coś dostanę na kolokwium to jak tak napiszę to mi gościu uzna Dobra to chyba będzie trzeba założyć że przeciwdziedzina to R\{1} bo wtedy będzie można wyznaczyć f⁻¹

Godzio: Jeśli było by napisane:

	−2
Funkcja f: R → R \ {1} określona wzorem f(x) =		+ 1
	x + 1

To jest surjektywna, jeśli byłoby: f: R → R to nie byłaby Wszystko zależy od polecenia. A co byłoby na kolokwium to już nie ode mnie zależy

PuRXUTM: Godzio możesz mi wytłumaczyć co to znaczy wyznacz f−1 na f(dom(f)) bo z tego co Janek napisał to nie za wiele zrozumiałem...

Godzio: Wyznaczenie funkcji odwrotnej jest standardowe tak jak napisał Janek

	x + 1
f−1(x) =
	1 − x

Dom(f) − dziedzina funkcji f f(Dom(f)) − przeciwdziedzina funkcji f Odwracając funkcję f : X → Y otrzymujemy f⁻¹: Y → X o ile funkcja odwrotna istnieje. Reszta tak jak wytłumaczył Janek

PuRXUTM: czyli f(dom(f))=f⁻¹(x) bo dalej średnio czaje...

Godzio: f(dom(f)) to przeciwdziedzina, czyli jakiś zbiór, a nie funkcja

PuRXUTM: czyli mam wyznaczyć zbiór wartości funkcji f czy f⁻¹

Godzio: Masz wyznaczyć f⁻¹ czyli funkcję odwrotną, Dom(f) to dziedzina f, która się staje przeciwdziedziną dla f⁻¹.

PuRXUTM: czyli dom(f)=R\{−1} ?

Godzio: Tak