Pomocy Ania: Blagam pomozcie 1.Trojkat prostokatny o przeciwprostokatnej AB jest wpisany okrag.Kat CAB ma miare 50 stopni .Wyznacz kat miedzy styczna do okregu poprowadzona w punkcie B i bokiem BC trojkata. 2.Wyzacz wspolrzedne srodka i promien okregu o rownaniu x2+y2+10x −12y +52=0 3.Napisz rownanie okregu o srodku S =(−3,6) i promieniu dlugosci odcinka o koncach A=(2,−3), B=(−5,−1) Z gory dziekuje za pomoc

AROB: Pomagam

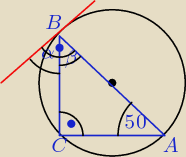
AROB: Zad. 1. β = 90⁰ − 50⁰ = 40⁰ α = 90⁰ − β = 50⁰ c.d.n.

AROB: Zad.2. x² + y² + 10x − 12y + 52 = 0 Równ. okręgu: x² + y² −2ax −2by + c = 0 Z przyrównania otrzymujemy: −2a = 10 ⇒ a = −5 −2b = −12 ⇒ b = 6 , c = 52 Czyli środek okręgu: S(−5,6). r = √a² + b² − c = √(−5)² + 6² − 52 = .....= 3 Zad. 3. S(−3,6) , A(2,−3) , B(−5,−1) r = IABI = √(x_B − x_A)² + (y_B − y_A)² = = √(−5−2)² + (−1+3)² = √49 + 4 = √53 Zatem równanie okręgu ma postać: (x − a )² + (y − b)² = r² (x + 3)² + (y − 6)² = 53