Funkcja kwadratowa bezendu: Wyznacz te wartości parametru m dla których równanie x²+mx+m=0 ma dwa różne pierwiastki, takie że ich iloczyn jest mniejszy od 6 Δ>0 x₁*x₂<6 Nie robię założenie odnośnie m ?

Piotr 10: Wg mnie jest okej. A po co założenie odnośnie m ?

bezendu: Często gęsto spotykam na internecie, że sprawdzany jest warunek liniowy i w tym wypadku m≠0 ?

Piotr 10: Ale warunek liniowy sprawdzasz jedynie gdy przy przy kwadracie masz m. Tutaj od razu masz narzuconą funkcję kwadratową. Jeżeli by było mx²+mx+m to sprawdzasz dla m=0 co się dzieje( wtedy jest funkcja liniowa)

Saizou : warunek liniowy sprawdzany może być wtedy kiedy jest parametr przy x², a tutaj tego nie ma

bezendu: Za chwilę kolejny przykład

bezendu: Dla jakich wartości parametru a równanie ma dwa różne pierwiastki jednakowych znaków ? x²+8x+a+2=0 Δ>0 x₁*x₂>0 ?

Piotr 10:

Saizou : jak dla mnie

bezendu: Dla jakich wartości parametru k równanie (k+1)x²+2x+1=0 ma dwa pierwiastki przeciwnych znaków ? Δ>0 k≠−1 x₁*x₂<0

Piotr 10:

bezendu: Dla jakich wartości parametru k dziedziną funkcji f(x)=√x²+x+k jest zbiór liczb rzeczywistych x²+x+k≥0 ?

Saizou : tak

Piotr 10: Tak i teraz jaka delta musi być ?

bezendu: Δ>0 ?

Saizou : a co z naszym kochanym zerem ?

bezendu: Czyli parabola będzie nad osią, a zero należy wykluczyć ?

Piotr 10: Δ≤0 taki warunek musi być. Przecież x²+x+k≥0 czyli x²+x+k=0 a więc tu delta 0

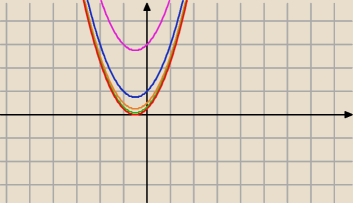
Mila: Wtedy wykres funkcji pod pierwiastkiem tak może wyglądać: Δ≤0

Saizou : ja tylko daję tematy do rozważań, żeby lepiej to zrozumieć

bezendu: W pierwszym kroku założenie ≥0 W drugim jaka ma być ta delta <0 czy tak jak napisał Piotrek ?

Lorak: Tak jak napisał Piotr 10

Mila: Δ≤0, zobacz wykresy. 22:38

	1		1
Dla Δ=0 ( dla k=		...) masz pod pierwiastkiem wyrażenie (x+		)2
	4		2

	1
czyli (x+		)2≥0 dla x∊R, to w porządku, pierwiastek istnieje.
	2

Zawsze, gdy masz wątpliwość, możesz sprawdzić w takim przypadku, co się dzieje gdy Δ=0.

bezendu: Ok, tak własnie będę robił. Dziękuję !

asdf: http://www.matmana6.pl/tablice_matematyczne/liceum/wielomiany/20-definicja_wielomianu_dzialania_na_wielomianach

bezendu: ?

asdf: jest to definicja wielomianu, dla stopnia drugiego: W₂(x) = a₀x² + a₁x + a₂, gdzie a₀ ≠ 0 dlatego czasem dla funkcji: W₂(x) = mx² + ax + C, z definicji: m ≠ 0, ale już dla parametrów a,C nie ma zadnych zalozen, dlatego jak będzie to = 0 to nic się nie stanie, niech a = C = 0: W₂(x) = mx² <−− nadal jest to wielomian drugiego stopnia

asdf: ale dla m = 0: W₂(x) = ax + C <−− nie jest to juz wielomian drugiego stopnia